
分析 确定所有基本事件的个数,其中两个骰子向上点数相同的基本事件的个数,即可求得概率
解答 解:根据题意,本题相当于有12个小球,编号为1的有3个小球,编号为2,4的各有一个小球,编号为3的有5个小球,编号为5的有2个小球,
从中任取一个小球共有12种取法,
取得小球为编号为1的概率为$\frac{3}{12}$=$\frac{1}{4}$,
取得小球为编号为2,4的概率为$\frac{1}{12}$,
取得小球为编号为3的概率为$\frac{5}{12}$,
取得小球为编号为5的概率为$\frac{2}{12}$=$\frac{1}{6}$,
所以得到1,2,3,4,5的概率分别是$\frac{1}{4}$,$\frac{1}{12}$,$\frac{5}{12}$,$\frac{1}{12}$,$\frac{1}{6}$.
故答案为:$\frac{1}{4}$,$\frac{1}{12}$,$\frac{5}{12}$,$\frac{1}{12}$,$\frac{1}{6}$.
点评 本题考查了古典概型的概率问题,转化为摸球问题是关键,属于基础题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
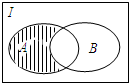
| A. | {-1,0,1} | B. | {2,3} | C. | {-2,2,3} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 将正奇数组成的数列{an},按下表排成5列:
将正奇数组成的数列{an},按下表排成5列:| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| 第四行 | … | … | 27 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
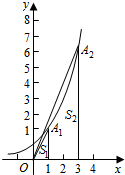
| A. | 2 | B. | 2.5 | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
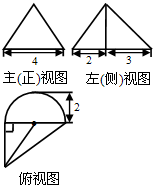 一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )
一个几何体的三视图如图所示,其主(正)视图是一个等边三角形,则这个几何体的体积为( )| A. | $12\sqrt{3}+4\sqrt{3}π$ | B. | $\frac{{4\sqrt{39}}}{3}+\frac{{4\sqrt{3}π}}{3}$ | C. | $12\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ | D. | $4\sqrt{3}+\frac{{4\sqrt{3}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com