
分析 通过1,$\sqrt{{S}_{n}}$,an成等差数列可知4Sn=${{a}_{n}}^{2}$+2an+1.
(Ⅰ)当n=1时,可得首项a1=1,当n≥2时,利用4an=4Sn-4Sn-1计算即得结论;
(Ⅱ)通过bn+1+(-1)nbn=2n-1计算可得bn+2+bn=(-1)n(2n-1)+2n+1、bn+3+bn+1=-(-1)n(2n+1)+2n+3,进而有b4k+1+b4k+2+b4k+3+b4k+4=16k+10,计算即可.
解答 解:由题可知:2$\sqrt{{S}_{n}}$=an+1,即4Sn=${{a}_{n}}^{2}$+2an+1.
(Ⅰ)当n=1时,4a1=${{a}_{1}}^{2}+2{a}_{1}+1$,解得a1=1,
当n≥2时,4an=4Sn-4Sn-1=(${{a}_{n}}^{2}$+2an+1)-(${{a}_{n-1}}^{2}$+2an-1+1),
化简得:${{a}_{n}}^{2}$-${{a}_{n-1}}^{2}$=2(an+an-1),
又∵an>0,∴an-an-1=2,
∴数列{an}的通项:an=2n-1;
(Ⅱ)由bn+1+(-1)nbn=2n-1得
bn+2=(-1)nbn+1+2n+1
=(-1)n[(-1)n-1bn+2n-1]+2n+1
=-bn+(-1)n(2n-1)+2n+1,
即bn+2+bn=(-1)n(2n-1)+2n+1,
也有bn+3+bn+1=-(-1)n(2n+1)+2n+3,
两式相加得:bn+bn+1+bn+2+bn+3=(-1)n(2n-1)+2n+1-(-1)n(2n+1)+2n+3,
设k为整数,整理得:b4k+1+b4k+2+b4k+3+b4k+4=-2(-1)4k+1+4(4k+1)+4=16k+10,
于是S60=$\sum_{k=0}^{14}(16k+10)$=1830.
点评 本题考查求数列的通项、前60项的和,考查运算求解能力,注意解题方法的积累,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Φ | B. | {x|-3<x<1} | C. | {x|-$\sqrt{2}$<x<1} | D. | {x|x2+2x-3<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<1} | B. | {x|x≥-2} | C. | {x|-2≤x<1} | D. | {x|-1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的图象关于直线x=$\frac{1}{2}$对称 | |
| B. | 函数f(x)的图象关关于点($\frac{1}{2}$,0)对称 | |
| C. | 函数f(x+1)在区间[2013,2014]内单调递增 | |
| D. | 函数f(x+1)的最小正周期为1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
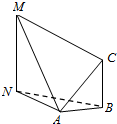 如图,为测量山高MN,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°已知山高BC=200m,则山高MN=300m.
如图,为测量山高MN,选择A和另一座山的山顶|PA|为测量观测点.从△ABC点测得MB=MC点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°已知山高BC=200m,则山高MN=300m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com