
(本小题满分12分)设函数f(x)=sinx, g(x)=ax,(a为常数),若f(x)≥g(x),对x∈[0, 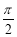 ]恒成立。
]恒成立。
(1)求a的最大值;
(2)对任意的锐角三角形ABC,均有sinA+sinB+sinC>M恒成立,求实数M的取值范围.
(1)a的最大值为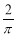 ;(2)M≤2.
;(2)M≤2.
【解析】
试题分析:(1)f(x)≥g(x)对x∈[0, 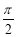 ]恒成立,转化成sinx≥ax对x∈[0,
]恒成立,转化成sinx≥ax对x∈[0, 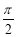 ]恒成立.
]恒成立.
当x=0时,sinx≥ax恒成立;
当x∈(0, 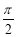 ]时,等价于a≤
]时,等价于a≤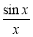 恒成立.
恒成立.
设 , x∈(0,
, x∈(0, 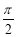 ],求得
],求得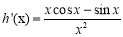
设(x)=xcosx-sinx,则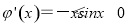 对x∈(0,
对x∈(0, 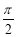 ]恒成立,
]恒成立,
根据(x)在(0, 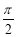 ]上单调递减,得到(x)min<(0)=0,即xcosx-sinx<0,
]上单调递减,得到(x)min<(0)=0,即xcosx-sinx<0,
得到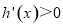 在(0,
在(0, 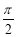 ]上恒成立,h(x) 在(0,
]上恒成立,h(x) 在(0, 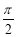 ]上单调递减,由h(x)min=h(
]上单调递减,由h(x)min=h(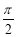 )=
)=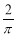 即得.
即得.
(2)由(1)知,当x∈(0, 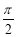 )时,有sinx>
)时,有sinx>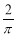 x成立,所以对任意锐角△ABC,有
x成立,所以对任意锐角△ABC,有
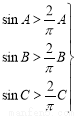 sinA+sinB+sinC>
sinA+sinB+sinC>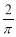 (A+B+C)=2,因此M≤2.
(A+B+C)=2,因此M≤2.
试题解析:(1)f(x)≥g(x)对x∈[0, 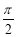 ]恒成立
]恒成立
即sinx≥ax对x∈[0, 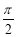 ]恒成立
]恒成立
当x=0时,sinx≥ax恒成立 1分
当x∈(0, 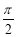 ]时,等价于a≤
]时,等价于a≤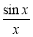 恒成立 2分
恒成立 2分
设h(x)=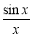 , x∈(0,
, x∈(0, 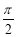 ]
]
则h ' (x)=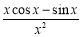
设(x)=xcosx-sinx,则 ' (x)=-xsinx<0对x∈(0, 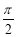 ]恒成立,
]恒成立,
∴(x)在(0, 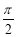 ]上单调递减,
]上单调递减,
(x)min<(0)=0,即xcosx-sinx<0,
∴h ' (x)>0在(0, 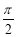 ]上恒成立,
]上恒成立,
∴h(x) 在(0, 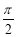 ]上单调递减
]上单调递减
∴h(x)min=h(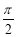 )=
)=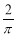 7分
7分
所以a≤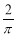 ,a的最大值为
,a的最大值为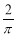 8分
8分
(2)由(1)知,当x∈(0, 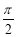 )时,有sinx>
)时,有sinx>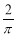 x成立,所以对任意锐角△ABC,有
x成立,所以对任意锐角△ABC,有
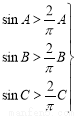 sinA+sinB+sinC>
sinA+sinB+sinC>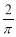 (A+B+C)
(A+B+C)
∵A+B+C=π, ∴sinA+sinB+sinC>2,
所以M≤2 12分
考点:1.应用导数研究函数的单调性、极值;2.不等式恒成立问题;3.等价转化思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:填空题
设点P(x, y)为函数y=x2-2(x>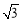 )图像上一动点,记m=
)图像上一动点,记m= , 则当m取最小值时,点P的坐标为 .
, 则当m取最小值时,点P的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省六校高三3月联考文科数学试卷(解析版) 题型:选择题
设双曲线 的右焦点为F(c, 0), 方程ax2+bx-c=0的两个实根分别为x1, x2,则点P(x1, x2) ( )
的右焦点为F(c, 0), 方程ax2+bx-c=0的两个实根分别为x1, x2,则点P(x1, x2) ( )
A.必在圆x2+y2=2内 B.必在圆x2+y2=2外
C.必在圆x2+y2=2上 D.以上三种情况都有可能
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南怀化市小学课改教育监测高三上学期期考试理科数学试卷(解析版) 题型:填空题
已知函数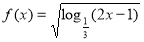 ,则
,则 的定义域为_______________ .
的定义域为_______________ .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省武汉市毕业生二月调研测试理科数学试卷(解析版) 题型:选择题
10件产品中有3件次品,不放回地抽取2次,在第1次抽出的是次品的前提下,则第2次抽出正品的概率是
A.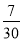 B.
B.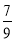 C.
C.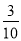 D.
D.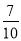
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com