
设P为双曲线x2-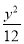 =1右支上的一点,F1、F2是该双曲线的左、右焦点,若|PF1|∶|PF2|=3∶2,则∠F1PF2的大小为________.
=1右支上的一点,F1、F2是该双曲线的左、右焦点,若|PF1|∶|PF2|=3∶2,则∠F1PF2的大小为________.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:选择题
如图所示,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:
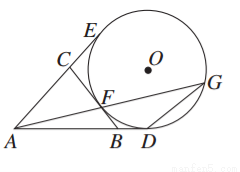
①AD+AE=AB+BC+CA;
②AF·AG=AD·AE;
③△AFB∽△ADG.
其中正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-2用样本估计总体(解析版) 题型:填空题
某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则x+y的值为________.
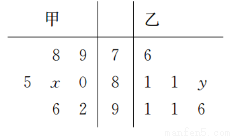
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-1随机抽样(解析版) 题型:选择题
某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查.现将800名学生从1到800进行编号.已知从33~48这16个数中取的数是39,则在第1小组1~16中随机抽到的数是( )
A.5 B.7 C.11 D.13
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:选择题
若直线mx+ny=4与⊙O:x2+y2=4没有交点,则过点P(m,n)的直线与椭圆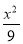 +
+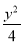 =1的交点个数是( )
=1的交点个数是( )
A.至多为1 B.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:选择题
设抛物线x2=4y与椭圆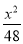 +
+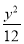 =1交于点E,F,则△OEF(O为坐标原点)的面积为( )
=1交于点E,F,则△OEF(O为坐标原点)的面积为( )
A.3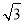 B.4
B.4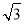 C.6
C.6 D.12
D.12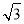
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:解答题
设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若|AB|=1.
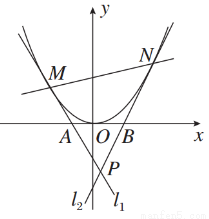
(1)求点P的轨迹方程;
(2)求证:△MNP的面积为一个定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:解答题
已知抛物线C:y2=2px(p>0)过点A(1,-2).
(1)求抛物线C的方程,并求其准线方程;
(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于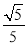 ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-4直线与圆、圆与圆的位置关系(解析版) 题型:解答题
已知圆C过点P(1,1),且与圆M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
(1)求圆C的方程;
(2)设Q为圆C上的一个动点,求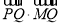 的最小值;
的最小值;
(3)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com