
如图所示,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:
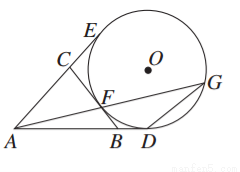
①AD+AE=AB+BC+CA;
②AF·AG=AD·AE;
③△AFB∽△ADG.
其中正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:解答题
如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.

(1)求证:BC2=AC·BP;
(2)若EC=2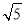 ,求PB的长.
,求PB的长.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:填空题
如图,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-1相似三角形判定及性质(解析版) 题型:填空题
如图,△ABC中,BC=4,∠BAC=120°,AD⊥BC,过B作CA的垂线,交CA的延长线于E,交DA的延长线于F,则AF=________.
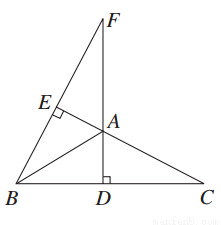
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-1相似三角形判定及性质(解析版) 题型:填空题
如图所示,矩形ABCD中,E是BC上的点,AE⊥DE,BE=4,EC=1,则AB的长为________.
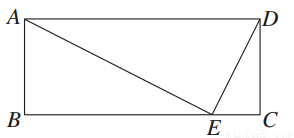
查看答案和解析>>
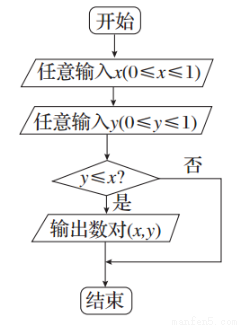
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-4算法初步(解析版) 题型:选择题
执行如图所示的程序框图,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出数对(x,y)的概率为( )
A. B.
B.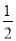 C.
C. D.
D.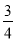
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-9圆锥曲线的综合问题(解析版) 题型:填空题
设P为双曲线x2-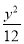 =1右支上的一点,F1、F2是该双曲线的左、右焦点,若|PF1|∶|PF2|=3∶2,则∠F1PF2的大小为________.
=1右支上的一点,F1、F2是该双曲线的左、右焦点,若|PF1|∶|PF2|=3∶2,则∠F1PF2的大小为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com