
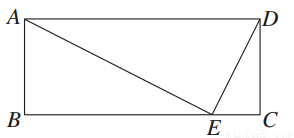
如图所示,矩形ABCD中,E是BC上的点,AE⊥DE,BE=4,EC=1,则AB的长为________.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-2直线与圆的位置关系(解析版) 题型:选择题
如图所示,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:
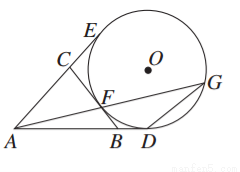
①AD+AE=AB+BC+CA;
②AF·AG=AD·AE;
③△AFB∽△ADG.
其中正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-1相似三角形判定及性质(解析版) 题型:选择题
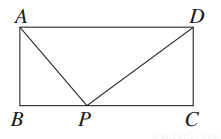
如图,在矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△PBA,△APD,△CDP两两相似,则a,b间的关系一定满足( )
A.a≥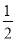 b B.a≥b C.a≥
b B.a≥b C.a≥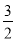 b D.a≥2b
b D.a≥2b
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:选4-1-1相似三角形判定及性质(解析版) 题型:选择题
如图,已知在?ABCD中,O1,O2,O3为对角线BD上三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于F,则AD∶FD等于( )
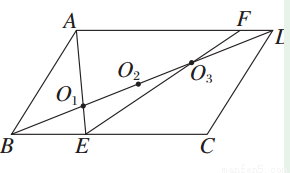
A.19∶2 B.9∶1
C.8∶1 D.7∶1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-2用样本估计总体(解析版) 题型:填空题
某中学从高三甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的中位数是83,则x+y的值为________.
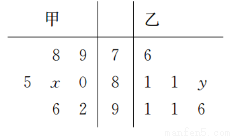
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:解答题
设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若|AB|=1.
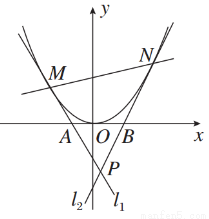
(1)求点P的轨迹方程;
(2)求证:△MNP的面积为一个定值,并求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com