
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
分析 对于①由f(x+2)=-f(x)可推知f(x+4)=f(x)得证.
对于②根据函数零点定理即可判断.
对于③首先判断x=0不是零点,其次说明函数f(x)在x>0和x<0上均有两个零点,对x>0的函数f(x)求导,对a讨论,说明a≤0不可能,a>0时,求出单调区间,求出极小值,令它小于0,解出a的范围,
对于④由题意,属于几何概型的概率求法,由此只要求出所有事件的区域长度以及满足条件的a的范围对应的区域长度,利用几何概型概率公式可求.
解答 解:对于①(1)∵f(x)=f(2-x),∴f(x+2)=f(2-(x+2))=f(-x)=-f(x)
∴f(x+4)=-f(x+2)=-f(-x)=f(x),
∴f(x)是以4为周期的函数,故正确,
对于②解:令f(x)=ex-x-6,
由表知f(2)=7.39-8<0,f(3)=20.09-9>0,
∴方程ex-x-6=0的一个根所在的区间为(2,3),故不正确,
对于③∵当x≥0时,f(x)=ex-ax,
∴f(0)=e0-0=1,即x=0不是零点,
∵函数f(x)是定义在R上的偶函数,
∴函数f(x)在x>0和x<0上有相同的零点个数,
∵函数f(x)在R上有且仅有4个零点,
∴f(x)在x>0上有且只有2个零点,
∵当x≥0时,f(x)=ex-ax,
导数f′(x)=ex-a,
当a≤0时,f′(x)≥0恒成立,
f(x)在x≥0上单调增,不可能有两个零点,
当a>0时,可得f(x)的增区间为(lna,+∞),减区间为(-∞,lna),
则f(lna)为极小值,令f(lna)<0,
即elna-alna<0,即a<alna,lna>1,
解得,a>e,
故a的取值范围是(e,+∞),故正确,
对于④:∵函数f(x)=-x2+ax+2在区间(1,+∞)上是单调减函数,
∴≤1,
∴a≤2,
∵实数a在区间[1,m](m>1)随机取值,
∴1≤a≤2,长度为1,
∵函数f(x)=-x2+ax+2在区间(1,+∞)上是单调减函数的概率为$\frac{1}{3}$,
∴1≤a≤m,长度为3,
∴m=4,
∴a∈(1,4),故正确,
故其中真命题是①③④,
故答案为:①③④
点评 本题主要考查函数的奇偶性及应用,考查函数的零点的概念和个数的判断,考查运用导数求函数的极值,考查几何概型,考查二次函数的单调性弄清极值与0的关系,是解题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:选择题
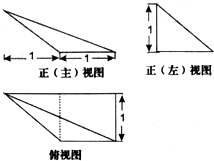
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
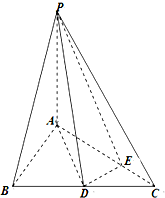 如图,三角形ABC是边长为4的正三角形,PA⊥底面ABC,$PA=\sqrt{7}$,点D是BC的中点,点E在AC上,且DE⊥AC.
如图,三角形ABC是边长为4的正三角形,PA⊥底面ABC,$PA=\sqrt{7}$,点D是BC的中点,点E在AC上,且DE⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ex-y+e-1=0 | B. | (e+1)x-y-1=0 | C. | x+y-e-1=0 | D. | 2e-y-e=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
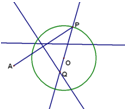 如图,圆O的半径为定长r,A是圆O外一个定点,P是圆上任意一点,线段AP的垂直平分线l和直线OP相交于点Q,当点P在圆上运动时,点Q的轨迹是双曲线.
如图,圆O的半径为定长r,A是圆O外一个定点,P是圆上任意一点,线段AP的垂直平分线l和直线OP相交于点Q,当点P在圆上运动时,点Q的轨迹是双曲线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com