
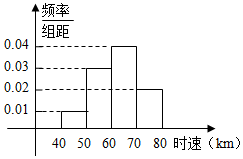
 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,分析 (1)由频率分布直方图能求出众数,平均数和中位数.
(2)由图可知,较高速度的2个时速段中的比值为2:1,由此利用分层抽样方法能求出各时段的抽取车辆.
(3)设事件A为两辆车的编号之和不大于10,利用对立事件概率计算公式能求出这两辆车的编号之和不大于10的概率.
解答 解:(1)∵频率分布直方图中[60,70)对应的小矩形最高,
∴众数为 $\frac{60+70}{2}$=65.(2分)
平均数为:45×0.1+55×0.3+65×0.4+75×0.2=62--------(4分)
中位数为:60+$\frac{1}{4}×10$=62.5-------(6分)
(2)由图可知,较高速度的2个时速段中的比值为2:1,
由分层抽样方法可知,
在速度较高的2个时速段中,按照分层抽样的方法,抽取6辆车做调查,
各时段的抽取车辆分别为4个和2个.-------(8分)
(3)设事件A为两辆车的编号之和不大于10,
则P(A)=$1-\frac{1}{15}=\frac{14}{15}$-----(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到$g(x)=\sqrt{2}sin(2x+\frac{π}{4})$的图象 | |
| B. | 若f(x1)=f(x2),则x1-x2=kπ,k∈Z | |
| C. | f(x)的图象关于直线$x=\frac{5}{8}π$对称 | |
| D. | f(x)的图象关于点$(-\frac{3}{8}π,0)$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既是等差数列又是等比数列 | B. | 既不是等差数列也不是等比数列 | ||
| C. | 是等差数列但不是等比数列 | D. | 是等比数列但不是等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com