
| A�� | ���ǵȲ��������ǵȱ����� | B�� | �Ȳ��ǵȲ�����Ҳ���ǵȱ����� | ||
| C�� | �ǵȲ����е����ǵȱ����� | D�� | �ǵȱ����е����ǵȲ����� |
���� ���¶��廯��{$\frac{\sqrt{5}+1}{2}$}��[$\frac{\sqrt{5}+1}{2}$]��Ȼ���ϵȲ����к͵ȱ����еĸ����жϣ�
��� �⣺������ɵ�{$\frac{\sqrt{5}+1}{2}$}=$\frac{\sqrt{5}+1}{2}-1=\frac{\sqrt{5}-1}{2}$��[$\frac{\sqrt{5}+1}{2}$]=1��
��${1}^{2}=\frac{\sqrt{5}-1}{2}��\frac{\sqrt{5}+1}{2}$��
��$\frac{\sqrt{5}-1}{2}��1��\frac{\sqrt{5}+1}{2}$���ɵȱ����У�
��$\frac{\sqrt{5}-1}{2}+\frac{\sqrt{5}+1}{2}��2$��
��{$\frac{\sqrt{5}+1}{2}$}��[$\frac{\sqrt{5}+1}{2}$]��$\frac{\sqrt{5}+1}{2}$�ǵȱ����е����ǵȲ����У�
��ѡ��D��
���� ���⿼��Ȳ����к͵ȱ����еĸ���ǻ����ļ����⣮


 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{5}$ | B�� | $\frac{4}{5}$ | C�� | $-\frac{3}{5}$ | D�� | $-\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
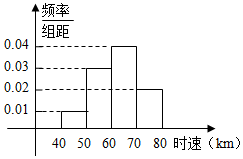 ��֪200������ͨ��ijһ�ι�·ʱ��ʱ�ٵ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
��֪200������ͨ��ijһ�ι�·ʱ��ʱ�ٵ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
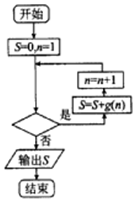 ��֪����f��x��=ax3+$\frac{1}{2}$x2��x=-1��ȡ�ü���ֵ����g��x��=$\frac{1}{f�䣨x��}$�������ͼ��ͼ��ʾ��������Ľ��S��$\frac{2014}{2015}$�����жϿ��п�������Ĺ���n���ж������ǣ�������
��֪����f��x��=ax3+$\frac{1}{2}$x2��x=-1��ȡ�ü���ֵ����g��x��=$\frac{1}{f�䣨x��}$�������ͼ��ͼ��ʾ��������Ľ��S��$\frac{2014}{2015}$�����жϿ��п�������Ĺ���n���ж������ǣ�������| A�� | n��2014�� | B�� | n��2015�� | C�� | n��2014�� | D�� | n��2015�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | ��-$\frac{1}{2}$��2�� | C�� | ��-2��2�� | D�� | ��-3��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | 1 | C�� | 3 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com