
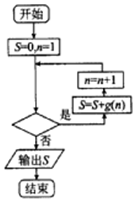
 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2014? | B. | n≤2015? | C. | n>2014? | D. | n>2015? |
分析 根据已知中的程序框图可得,该程序的功能是计算并输出变量S的值,模拟程序的运行过程,可得答案.
解答 解:函数f(x)=ax3+$\frac{1}{2}$x2,在x=-1处取得极大值,
即f′(x)=3ax2+x的零点为-1,
即 3a-a=0,解得:a=$\frac{1}{3}$,
故f′(x)=x2+x,
故g(x)=$\frac{1}{f′(x)}$=$\frac{1}{x}$-$\frac{1}{x+1}$,
则S=g(1)+g(2)+g(3)+…+g(k)=1-$\frac{1}{k+1}$=$\frac{k}{k+1}$,
若输出的结果S>$\frac{2014}{2015}$,则k>2015,
故进行循环的条件应为n≤2015?,
故选:B.
点评 本题以程序框图为载体,考查了函数在某点取得极值的条件,数列求和,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既是等差数列又是等比数列 | B. | 既不是等差数列也不是等比数列 | ||
| C. | 是等差数列但不是等比数列 | D. | 是等比数列但不是等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x0与f(x)=1 | B. | f(x)=$\sqrt{{x}^{2}}$-1与f(x)=|x|-1 | ||
| C. | f(x)=$\frac{{x}^{2}-4}{x+2}$与f(x)=x-2 | D. | f(x)=$\sqrt{(x-1)(x-2)}$与f(x)=$\sqrt{x-1}$$\sqrt{x-2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com