
分析 (1)当a<0时,求出函数$y=\sqrt{f(x)}$定义域与值域,利用定义域与值域完全相同,求a的值;
(2)当a>0时,分类讨论求函数g(x)=f(x)-2x-|x-a|的最小值h(a).
解答 解:(1)当a<0时,$y=\sqrt{f(x)}$定义域为[0,-$\frac{1}{a}$].
$y=\sqrt{f(x)}$=$\sqrt{a(x+\frac{1}{2a})^{2}-\frac{1}{4a}}$值域为[0,$\sqrt{-\frac{1}{4a}}$],
∴$\frac{1}{a}$=$\sqrt{-\frac{1}{4a}}$,∴a=-4;
(2)g(x)=$\left\{\begin{array}{l}{a{x}^{2}-2x+a,x≥a}\\{a{x}^{2}-a,x<a}\end{array}\right.$,
①0≤a≤1,$\frac{1}{a}≥a$,x≥a,g(x)min=g($\frac{1}{a}$)=a-$\frac{1}{a}$,x<a,g(x)min=g(0)=-a,
a-$\frac{1}{a}$≥-a,∴$\frac{\sqrt{2}}{2}$≤a≤1,h(a)=-a;
a-$\frac{1}{a}$<-a,∴0<a<$\frac{\sqrt{2}}{2}$,h(a)=a-$\frac{1}{a}$;
②a>1,$\frac{1}{a}$<a,x≥a,g(x)min=g(a),x<a,g(x)min=g(0)=-a,函数在[0,a]上单调递增,
∴h(a)=-a;
综上所述,h(a)=$\left\{\begin{array}{l}{a-\frac{1}{a},0<a<\frac{\sqrt{2}}{2}}\\{-a,a≥\frac{\sqrt{2}}{2}}\end{array}\right.$.
点评 本题考查函数的定义域与值域,考查函数的最小值,考查分类讨论的数学思想,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
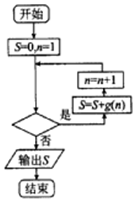 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.程序框图如图所示,若输出的结果S>$\frac{2014}{2015}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2014? | B. | n≤2015? | C. | n>2014? | D. | n>2015? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-$\frac{1}{2}$,2) | C. | (-2,2) | D. | (-3,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
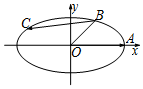 如图,椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右顶点,B是该椭圆在第一象限部分上的一点,且∠AOB=$\frac{π}{4}$.若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为[-9,3].
如图,椭圆的方程为$\frac{x^2}{6}+\frac{y^2}{2}$=1,A是其右顶点,B是该椭圆在第一象限部分上的一点,且∠AOB=$\frac{π}{4}$.若点C是椭圆上的动点,则$\overrightarrow{OA}•\overrightarrow{BC}$的取值范围为[-9,3].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com