
分析 作PM⊥准线l,M为垂足,由抛物线的定义可得|PA|+|PF|=|PA|+|PM|,故当P,A,M三点共线时,|PA|+|PM|最小为|AM|,此时,P点的纵坐标为2$\sqrt{3}$,代入抛物线的方程可求得P点的横坐标为2,从而得到P点的坐标.
解答  解:由题意可得F($\frac{3}{2}$,0 ),准线方程为x=-$\frac{3}{2}$,
解:由题意可得F($\frac{3}{2}$,0 ),准线方程为x=-$\frac{3}{2}$,
作PM⊥准线l,M为垂足,
由抛物线的定义可得|PA|+|PF|=|PA|+|PM|,
故当P,A,M三点共线时,
|PA|+|PM|最小为|AM|=$\frac{7}{2}$-(-$\frac{3}{2}$)=5,
此时,P点的纵坐标为2$\sqrt{3}$,代入抛物线的方程
可求得P点的横坐标为2,
故P点的坐标为(2,2$\sqrt{3}$),
故答案为:5,(2,2$\sqrt{3}$).
点评 本题主要考查抛物线的定义、标准方程,以及简单性质的应用,判断当P,A,M三点共线时,|PA|+|PM|最小为|AM|,是解题的关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线G的顶点在原点,焦点F为圆(x-1)2+y2=1的圆心.设过点F的直线与抛物线G及圆F依次交于如图中所示的A,B,C,D四点.
已知抛物线G的顶点在原点,焦点F为圆(x-1)2+y2=1的圆心.设过点F的直线与抛物线G及圆F依次交于如图中所示的A,B,C,D四点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )
如图,在棱长为1正四面体S-ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O-PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
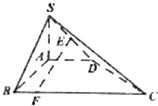 在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.
在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com