
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
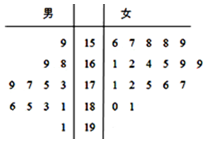 某小学对五年级的学生进行体质测试,已测得五年级一班30名学生的跳远成绩(单位:cm),用茎叶图统计如图,男生成绩在175cm以上(包括175cm)定义为合格,成绩在175cm以下(不含175cm)定义为“不合格”;女生成绩在165以上(包括165cm)定义为“合格”,成绩在165cm以下(不含165cm)定义为“不合格”.
某小学对五年级的学生进行体质测试,已测得五年级一班30名学生的跳远成绩(单位:cm),用茎叶图统计如图,男生成绩在175cm以上(包括175cm)定义为合格,成绩在175cm以下(不含175cm)定义为“不合格”;女生成绩在165以上(包括165cm)定义为“合格”,成绩在165cm以下(不含165cm)定义为“不合格”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinα)>f(sinβ) | B. | f(sinα)<f(cosβ) | C. | f(cosα)<f(cosβ) | D. | f(sinα)>f(cosβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
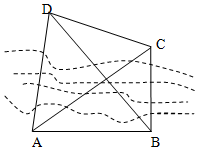 如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.则C,D两点之间的距离为10$\sqrt{10}$ m.
如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.则C,D两点之间的距离为10$\sqrt{10}$ m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (2,+∞) | C. | (-∞,2) | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $1+\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | $3+\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com