
分析 由sinB=sin(A+C)便可得出cosC=0,进而得出$C=\frac{π}{2}$,画出图形,从而得到$\overrightarrow{EB}=-\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})$,$\overrightarrow{EA}=-\frac{1}{2}\overrightarrow{AC}$,这样代入$\overrightarrow{EB}•\overrightarrow{EA}$进行数量积的运算即可求出该数量积的值.
解答 解:sinB=sin(A+C)=sinAcosC+cosAsinC=cosAsinC;
∴sinAcosC=0;
∴cosC=0,$C=\frac{π}{2}$,如图: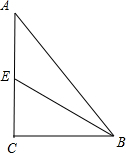
$\overrightarrow{EB}•\overrightarrow{EA}=[-\frac{1}{2}(\overrightarrow{BA}+\overrightarrow{BC})]•$$(-\frac{1}{2}\overrightarrow{AC})$
=$\frac{1}{4}(\overrightarrow{BA}•\overrightarrow{AC}+\overrightarrow{BC}•\overrightarrow{AC})$
=$\frac{1}{4}(-\overrightarrow{AB}•\overrightarrow{AC}+0)$
=-1.
故答案为:-1.
点评 考查两角和的正弦公式,三角形内角的范围,向量加法的平行四边形法则,以及向量数乘的几何意义,向量数量积的运算.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π | B. | 是奇函数 | ||
| C. | 在区间$(-\frac{1}{12}π,\frac{5}{12}π)$上单调递减 | D. | $(\frac{5}{12}π,0)$为其图象的一个对称中心 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
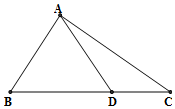 如图,在△ABC中,AB=2,3acosB-bcosC=ccosB,点D在线段BC上.
如图,在△ABC中,AB=2,3acosB-bcosC=ccosB,点D在线段BC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com