
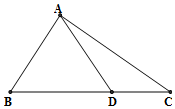
 如图,在△ABC中,AB=2,3acosB-bcosC=ccosB,点D在线段BC上.
如图,在△ABC中,AB=2,3acosB-bcosC=ccosB,点D在线段BC上.分析 (Ⅰ)由三角形内角和定理,两角和的正弦函数公式,正弦定理化简已知等式可得3sinAcosB=sinA,结合sinA>0,可求$cosB=\frac{1}{3}$,利用同角三角函数基本关系式可求sinB,进而可求$∠ADB=\frac{π}{4}$,由正弦定理即可求得AD的值.
(Ⅱ)设DC=a,则BD=2a,利用已知及三角形面积公式可求a,利用余弦定理可求AC,由正弦定理可得$sin∠CAD=\frac{{\sqrt{2}}}{4}sin∠ADC$,结合sin∠ADB=sin∠ADC,即可求值得解.
解答 (本小题满分12分)
解:(Ⅰ)∵3acosB-bcosC=ccosB,
∴3sinAcosB=sinCcosB+sinBcosC,3sinAcosB=sin(B+C),
∵B+C=π-A,
∴3sinAcosB=sinA,
∵A∈(0,π),
∴sinA>0,$cosB=\frac{1}{3}$.…(2分)
∵B∈(0,π),
∴$sinB=\frac{{2\sqrt{2}}}{3}$.…(3分)
∵$∠ADC=\frac{3π}{4}$,
∴$∠ADB=\frac{π}{4}$,
在△ABD中,由正弦定理得,$\frac{AD}{sinB}=\frac{AB}{sin∠ADB}$,
∴$\frac{AD}{{\frac{{2\sqrt{2}}}{3}}}=\frac{2}{{\frac{{\sqrt{2}}}{2}}}$,$AD=\frac{8}{3}$.…(6分)
(Ⅱ)设DC=a,则BD=2a,
∵BD=2DC,△ACD的面积为$\frac{4}{3}\sqrt{2}$,
∴${S_{△ABC}}=3{S_{△ACD}}=4\sqrt{2}$,
∴$4\sqrt{2}=\frac{1}{2}×2×3a×\frac{{2\sqrt{2}}}{3}$,
∴a=2.…(8分)
∴$AC=\sqrt{4+36-2×2×6×\frac{1}{3}}=4\sqrt{2}$,由正弦定理可得$\frac{4}{sin∠BAD}=\frac{2}{sin∠ADB}$,
∴$sin∠BAD=\frac{1}{2}sin∠ADB$.$\frac{2}{sin∠CAD}=\frac{{4\sqrt{2}}}{sin∠ADC}$,
∴$sin∠CAD=\frac{{\sqrt{2}}}{4}sin∠ADC$,
∵sin∠ADB=sin∠ADC,
∴$\frac{sin∠BAD}{sin∠CAD}=\sqrt{2}$.…(12分)
点评 本题主要考查了三角形内角和定理,两角和的正弦函数公式,正弦定理,同角三角函数基本关系式,三角形面积公式,余弦定理在解三角形中的综合应用,考查了转化思想,熟练掌握相关公式定理的应用是解题的关键,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
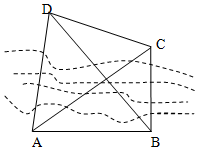 如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.则C,D两点之间的距离为10$\sqrt{10}$ m.
如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.则C,D两点之间的距离为10$\sqrt{10}$ m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com