
分析 (1)利用an=Sn-Sn-1求解;(2)要使Tn≤m对于一切的正整数n恒成立,只需m≥{Tn}中的最大值即可;(3)求解有关正整数n的不等式.
解答 解:(1)由已知,得${S_n}=\frac{3}{2}{n^2}+\frac{3}{2}n$…(1分)
当n≥2时,an=Sn-Sn-1=$\frac{3}{2}{n^2}+\frac{3}{2}n-[\frac{3}{2}{(n-1)^2}+\frac{3}{2}(n-1)]$=3n…(2分)
当n=1时,a1=S1=3.∴an=3n…(3分)
(2)解法一:${T_n}=\frac{9n(n+1)}{2^n}⇒$${T_{n+1}}-{T_n}=\frac{9(n+1)(n+2)}{{{2^{n+1}}}}-\frac{9n(n+1)}{2^n}=\frac{9(n+1)(2-n)}{{{2^{n+1}}}}$.(4分)
当n=1时,Tn+1>Tn,即T2>T1;当n=2时,Tn+1=Tn,即T3=T2;
当n≥3时,Tn+1<Tn,即Tn<Tn-1<…<T4<T3…(6分)
∴{Tn}中的最大值为${T_2}={T_3}=\frac{27}{2}$,
要使Tn≤m对于一切的正整数n恒成立,只需$\frac{27}{2}≤m$∴$m≥\frac{27}{2}$…(7分)
解法二:${T_n}=\frac{{{a_n}•{a_{n+1}}}}{2^n}=\frac{9n(n+1)}{2^n}$$⇒\frac{{{T_{n+1}}}}{T_n}=\frac{{\frac{9(n+1)(n+2)}{{{2^{n+1}}}}}}{{\frac{9n(n+1)}{2^n}}}=\frac{n+2}{2n}$…(4分)
当n=1,2时,Tn+1≥Tn;当n≥3时,n+2<2n⇒Tn+1<Tn
∴n=1时,T1=9;n=2,3时,${T_2}={T_3}=\frac{27}{2}$n≥4时,Tn<T3…(6分)
∴{Tn}中的最大值为${T_2}={T_3}=\frac{27}{2}$,
要使Tn≤m对于一切的正整数n恒成立,只需$\frac{27}{2}≤m$∴$m≥\frac{27}{2}$…(7分)
(3)${b_n}={2^{a_n}}={2^{3n}}=8{\;}^n⇒{K_n}=\frac{{8(1-{8^n})}}{1-8}=\frac{8}{7}(8{\;}^n-1)$…(8分)
将Kn代入$\frac{{{K_n}-t{b_n}}}{{{K_{n+1}}-t{b_{n+1}}}}<\frac{1}{16}$,化简得,$\frac{{({\frac{8}{7}-t}){8^n}-\frac{8}{7}}}{{({\frac{8}{7}-t}){8^n}-\frac{1}{7}}}<\frac{1}{2}$(﹡)…(9分)
若t=1时,$\frac{{\frac{8^n}{7}-\frac{8}{7}}}{{\frac{8^n}{7}-\frac{1}{7}}}<\frac{1}{2},即\frac{8^n}{7}<\frac{15}{7}$,显然n=1时成立; …(10分)
若t>1时,$({\frac{8}{7}-t}){8^n}-\frac{1}{7}<0$(﹡)式化简为$({\frac{8}{7}-t}){8^n}>\frac{15}{7}$不可能成立 …(11分)
综上,存在正整数n=1,t=1使$\frac{{{K_n}-t{b_n}}}{{{K_{n+1}}-t{b_{n+1}}}}<\frac{1}{16}$成立 …(12分)
点评 本题考察了数列中an和sn的转换关系式,数列中恒成立问题的处理方法,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要 | D. | 既非充分也非必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
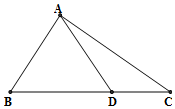 如图,在△ABC中,AB=2,3acosB-bcosC=ccosB,点D在线段BC上.
如图,在△ABC中,AB=2,3acosB-bcosC=ccosB,点D在线段BC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com