
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据各个函数的解析式先求出定义域,由对数、指数的运算分别化简后,根据函数奇偶性的定义进行判断.
解答 解:①、由$\frac{1-x}{1+x}>0$得(1-x)(1+x)>0,解得-1<x<1,
则函数f(x)的定义域是(-1,1),
且f(-x)=ln$\frac{1+x}{1-x}$=-ln$\frac{1-x}{1+x}$=-f(-x),所以函数f(x)是奇函数;
②、函数g(x)的定义域是R,
且g(-x)=$\frac{1}{2}$(e-x+ex)=g(x),则函数g(x)是偶函数;
③、因$\sqrt{1+{x}^{2}}-x>0$恒成立,所以函数h(x)的定义域是R,
且h(-x)=lg($\sqrt{1+{x}^{2}}+x$)=lg$\frac{1}{\sqrt{1+{x}^{2}}-x}$=-lg($\sqrt{1+{x}^{2}}$-x)=-h(x),
所以函数h(x)是奇函数;
④、由2x-1≠0得x≠0,函数h(x)的定义域是{x|x≠0},
且m(-x)=$\frac{1}{{2}^{-x}-1}$$+\frac{1}{2}$=$\frac{{2}^{x}}{{1-2}^{x}}+\frac{1}{2}$=$\frac{{-2}^{x}}{{2}^{x}-1}+\frac{1}{2}$
=$\frac{{-(2}^{x}-1)-1}{{2}^{x}-1}+\frac{1}{2}$=-$\frac{1}{{2}^{x}-1}$-$\frac{1}{2}$=-m(x),
所以函数m(x)是奇函数,
综上可得,奇函数为①③④,共3个,
故选C.
点评 本题主要考查函数奇偶性的判断,对数、指数的运算,以及函数的定义域,根据函数奇偶性的定义以及定义域的对称性是解决本题的关键,考查化简、变形能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
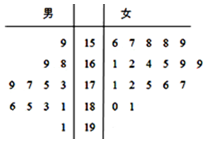 某小学对五年级的学生进行体质测试,已测得五年级一班30名学生的跳远成绩(单位:cm),用茎叶图统计如图,男生成绩在175cm以上(包括175cm)定义为合格,成绩在175cm以下(不含175cm)定义为“不合格”;女生成绩在165以上(包括165cm)定义为“合格”,成绩在165cm以下(不含165cm)定义为“不合格”.
某小学对五年级的学生进行体质测试,已测得五年级一班30名学生的跳远成绩(单位:cm),用茎叶图统计如图,男生成绩在175cm以上(包括175cm)定义为合格,成绩在175cm以下(不含175cm)定义为“不合格”;女生成绩在165以上(包括165cm)定义为“合格”,成绩在165cm以下(不含165cm)定义为“不合格”.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
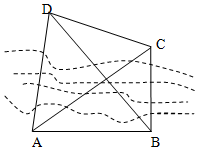 如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.则C,D两点之间的距离为10$\sqrt{10}$ m.
如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.则C,D两点之间的距离为10$\sqrt{10}$ m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 70 | 40 |
| 不需要 | 30 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com