
���� ���������������ɽ���֪��ʽչ����������������������ʽ������ģ��ƽ������������ƽ������������нǵ����ң�����нǣ�
��� �⣺��$\overrightarrow{a}$��$\overrightarrow{b}$�ļн�Ϊ�ȣ�
��|$\overrightarrow{a}$|=2��|$\overrightarrow{b}$|=1��|$\overrightarrow{a}$-2$\overrightarrow{b}$|=2$\sqrt{3}$��
��|$\overrightarrow{a}$-2$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+4|$\overrightarrow{b}$|2-4|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos��=4+4-4��2��1��cos��=12��
��cos��=-$\frac{1}{2}$��
��0��ܦȡ�180�㣬
���=120�㣬
�ʴ�Ϊ��120�㣮
���� ���⿼�������������ɡ�������������������ʽ����������ģ��ƽ������������ƽ����


 Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
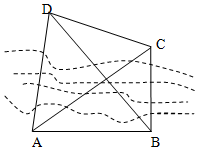 ��ͼ��Ҫ�����Ӷ�C��D�����ľ��룬�ںӱ�һ��ѡ������A��B�����AB�ľ���Ϊ20$\sqrt{3}$m����DAB=75�㣬��CAB=30�㣬AB��BC����ABD=60�㣮��C��D����֮��ľ���Ϊ10$\sqrt{10}$ m��
��ͼ��Ҫ�����Ӷ�C��D�����ľ��룬�ںӱ�һ��ѡ������A��B�����AB�ľ���Ϊ20$\sqrt{3}$m����DAB=75�㣬��CAB=30�㣬AB��BC����ABD=60�㣮��C��D����֮��ľ���Ϊ10$\sqrt{10}$ m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��2�� | B�� | ��2��+�ޣ� | C�� | ��-�ޣ�2�� | D�� | ��-�ޣ�2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $1+\sqrt{3}$ | C�� | 3$\sqrt{3}$ | D�� | $3+\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �Ա� �Ƿ���Ҫ־Ը�� | �� | Ů |
| ��Ҫ | 70 | 40 |
| ����Ҫ | 30 | 60 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �㽭���ӡ����ܰ��ֵܡ����ս�Ŀ�������ʣ����ó��ķ�ʽ | |
| B�� | �˽�ij�泡�������ƽ�����������ó��ķ�ʽ | |
| C�� | �˽�iphone6s�ֻ���ʹ�������������ղ�ķ�ʽ | |
| D�� | �˽�һ��������ɲ�����ܣ������ղ�ķ�ʽ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com