
分析 (1)根据α、β的取值范围,利用同角的三角函数关系,求出tan(α+$\frac{β}{2}$)的值,再利用二倍角公式计算tan(2α+β)的值;
(2)根据α、β的取值范围,利用同角的三角函数关系和三角恒等变换,求出cos($\frac{3α}{2}$-$\frac{β}{2}$)的值,再计算cos(3α-β)的值.
解答 解:(1)∵0<α<$\frac{π}{2}$,$\frac{π}{2}$<β<π,
∴$\frac{π}{4}$<α+$\frac{β}{2}$<π,
又cos(α+$\frac{β}{2}$)=$\frac{\sqrt{3}}{3}$,
∴sin(α+$\frac{β}{2}$)=$\sqrt{1{-(\frac{\sqrt{3}}{3})}^{2}}$=$\frac{\sqrt{6}}{3}$,
∴tan(α+$\frac{β}{2}$)=$\frac{sin(α+\frac{β}{2})}{cos(α+\frac{β}{2})}$=$\frac{\frac{\sqrt{6}}{3}}{\frac{\sqrt{3}}{3}}$=$\sqrt{2}$,
∴tan(2α+β)=$\frac{2tan(α+\frac{β}{2})}{1{-tan}^{2}(α+\frac{β}{2})}$=$\frac{2×\sqrt{2}}{1{-(\sqrt{2})}^{2}}$=-2$\sqrt{2}$;
(2)∵0<α<$\frac{π}{2}$,∴0<$\frac{α}{2}$<$\frac{π}{4}$,
又$\frac{π}{2}$<β<π,∴-π<-β<-$\frac{π}{2}$,
∴-π<$\frac{α}{2}$-β<-$\frac{π}{4}$;
又cos($\frac{α}{2}$-β)=$\frac{1}{3}$,
∴sin($\frac{α}{2}$-β)=-$\sqrt{1{-(\frac{1}{3})}^{2}}$=-$\frac{2\sqrt{2}}{3}$,
∴cos($\frac{3α}{2}$-$\frac{β}{2}$)=cos[(α+$\frac{β}{2}$)+($\frac{α}{2}$-β)]
=cos(α+$\frac{β}{2}$)cos($\frac{α}{2}$-β)-sin(α+$\frac{β}{2}$)sin($\frac{α}{2}$-β)
=$\frac{\sqrt{3}}{3}$×$\frac{1}{3}$-$\frac{\sqrt{6}}{3}$×(-$\frac{2\sqrt{2}}{3}$)=$\frac{5\sqrt{3}}{9}$.
∴cos(3α-β)=2${cos}^{2}(\frac{3α}{2}-\frac{β}{2})$-1=2×${(\frac{5\sqrt{3}}{9})}^{2}$-1=$\frac{23}{27}$.
点评 本题考查了同角的三角函数关系与三角恒等变换的应用问题,是综合性题目.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-$\sqrt{2}$ | B. | 1 | C. | 2$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
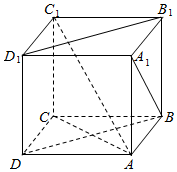 如图,对于正方体ABCD-A1B1C1D1,给出下列四个结论:
如图,对于正方体ABCD-A1B1C1D1,给出下列四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知D是等腰直角三角形ABC斜边BC的中点,AB=$\sqrt{6}$,P是平面ABC外一点,PC⊥平面ABC,DE⊥BP于E,DE=1.
如图,已知D是等腰直角三角形ABC斜边BC的中点,AB=$\sqrt{6}$,P是平面ABC外一点,PC⊥平面ABC,DE⊥BP于E,DE=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com