
分析 (I)对于曲线C:利用sin2θ+cos2θ=1即可把参数方程化为普通方程,根据θ∈[0,π],可得0≤y≤1,它的轨迹是焦点在x轴上的上半椭圆.
(II)对b分类讨论:当直线l经过点(2,0)时,b=-2,此时直线与椭圆只有一个公共点.当直线l经过点(-2,0)时,b=2,此时直线l与椭圆有两个公共点.当-2≤b<2时,满足直线l与椭圆只有一个公共点.设直线y=x+b与椭圆相切时只有一个公共点.
解答  解:(I)对于曲线C:∵sin2θ+cos2θ=1,∴$\frac{{x}^{2}}{4}+{y}^{2}$=1,∵θ∈[0,π],∴sinθ∈[0,1],∴0≤y≤1,
解:(I)对于曲线C:∵sin2θ+cos2θ=1,∴$\frac{{x}^{2}}{4}+{y}^{2}$=1,∵θ∈[0,π],∴sinθ∈[0,1],∴0≤y≤1,
∴曲线C的普通方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1,0≤y≤1,它的轨迹是焦点在x轴上的上半椭圆.
(II)当直线l经过点(2,0)时,b=-2,此时直线与椭圆只有一个公共点.当直线l经过点(-2,0)时,b=2,
此时直线l与椭圆有两个公共点.当-2≤b<2时,满足直线l与椭圆只有一个公共点.
设直线y=x+b与椭圆相切,
把y=x+b代入椭圆方程可得:x2+4(x+b)2=4,
化为5x2+8bx+4b2-4=0.
令△=64b2-20(4b2-4)=0,
解得b=$\sqrt{5}$$(-\sqrt{5}舍去)$,此时直线l与椭圆只有一个公共点.
综上可得:b∈[-2,2)∪$\{\sqrt{5}\}$.
点评 本题考查了参数方程化为普通方程用、直线与椭圆相交相切问题,考查了数形结合方法、分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
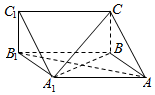 如图,在三棱柱ABC-A1B1C1中,A1A=AB,CB⊥A1ABB1.
如图,在三棱柱ABC-A1B1C1中,A1A=AB,CB⊥A1ABB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
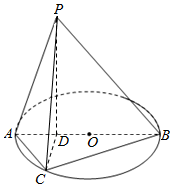 如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=$\frac{1}{3}$DB,点C为圆O上一点,且BC=$\sqrt{3}$AC.点P在圆O所在平面上的正投影为点D,PD=DB.
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=$\frac{1}{3}$DB,点C为圆O上一点,且BC=$\sqrt{3}$AC.点P在圆O所在平面上的正投影为点D,PD=DB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com