练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知复数z=$\frac{2-2i}{1+i}$，则z的共轭复数的虚部等于（　　）
    A．2iB．-2iC．2D．-2

    分析 利用复数代数形式的乘除运算化简，求得$\overline{z}$，则答案可求．

    解答 解：z=$\frac{2-2i}{1+i}$=$\frac{（2-2i）（1-i）}{（1+i）（1-i）}=\frac{2（1-i）^{2}}{2}=-2i$，
    ∴$\overline{z}=2i$，
    z的共轭复数的虚部等于2．
    故选：C．

    点评 本题考查复数代数形式的乘除运算，考查共轭复数的概念，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=ln（x+a），其中a＞0，若方程f（x）=x有唯一解．
    （1）求函数f（x）的解析式；
    （2）若k≤-$\frac{1}{2}$，f1（x）=f（x）-x，证明：对任意的x∈[0，+∞），f1（x）≥kx2恒成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知某地区小学生3500人，初中生4500人，高中生2000人，近视情况如图所示．为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为200，20．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

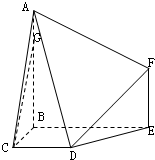    17．如图，在多面体ABCDEF中，BA⊥BE，BA⊥BC，BE⊥BC，AB∥EF，CD∥BE，AB=BE=2，BC=CD=EF=1，G在线段AB上，且BG=3GA．
    （1）求证：CG∥平面ADF；
    （2）求直线DE与平面ADF所成的角的正弦值；
    （3）求锐二面角B-DF-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分（单位：分）若甲运动员的中位数为a，乙运动员的众数为b，则a-b的值是8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知函数f（x）=sinωx（ω＞0）的图象与直线y=1的相邻交点之间的距离为π，f（x）的图象向左平移$\frac{π}{6}$个单位后，得到函数y=g（x）的图象．下列关于y=g（x）的说法正确的是（　　）
    A．图象关于点$（{-\frac{π}{3}，0}）$中心对称B．图象关于$x=-\frac{π}{6}$轴对称
    C．在区间$[{-\frac{5π}{12}，-\frac{π}{6}}]$上单调递增D．在区间$[{-\frac{π}{6}，\frac{π}{3}}]$上单调递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．过点$（2，\frac{π}{3}）$且垂直于极轴的直线的极坐标方程为ρcosθ=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．在△ABC中，设角A、B、C的对边分别为a、b、c，已知$\overrightarrow m=（a，\frac{c}{2}）$，$\overrightarrow n=（cosC，1）$，且$\overrightarrow m•\overrightarrow n=b$．
    （Ⅰ）求角A的大小；
    （Ⅱ）若a=3，求△ABC的面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知袋子中放有大小和形状相同的小球若干，其标号为0的小球1个，标号为1的小球1个，标号为2的小球n个．若从袋子中随机抽取1个小球，取到标号为2的小球的概率是$\frac{1}{2}$．
    （Ⅰ）求n的值；
    （Ⅱ）从袋子中不放回地随机抽取2个球，记第一次取出的小球标号为a，第二次取出的小球标号为b．
    ①记“2≤a+b≤3”为事件A，求事件A的概率；
    ②在区间[0，2]内任取2个实数x，y，求事件“x2+y2＞（a-b）2恒成立”的概率．

    查看答案和解析>>

    同步练习册答案