
 以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分(单位:分)若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是8.
以下茎叶图记录了某赛季甲、乙两名篮球运动员参加11场比赛的得分(单位:分)若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是8. 科目:高中数学 来源: 题型:选择题
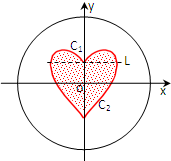 如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )
如图所示,一个圆形靶子的中心是一个“心形”图案,其中“心形”图案是由上边界C1(虚线L上方部分)与下边界C2(虚线L下方部分)围成,曲线C1是函数y=$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{4}{5}}$ 的图象,曲线C2是函数y=-$\sqrt{1-{x}^{2}}$+x${\;}^{\frac{2}{7}}$ 的图象,圆的方程为x2+y2=8,某人向靶子射出一箭(假设此人此箭一定能射中靶子且射中靶中任何一点是等可能的),则此箭恰好命中“心形”图案的概率为( )| A. | $\frac{1}{4}$-$\frac{1}{18π}$ | B. | $\frac{1}{16}$-$\frac{1}{18π}$ | C. | $\frac{1}{8}$+$\frac{1}{18π}$ | D. | $\frac{1}{8}$+$\frac{36}{35π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
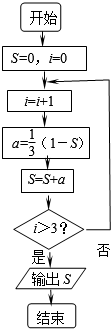
| A. | $\frac{65}{81}$ | B. | $\frac{19}{27}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com