
分析 (1)根据它们获得冠军的概率分别为$\frac{1}{2}$,$\frac{1}{3}$,$\frac{2}{3}$.求得1个,2个,3个冠军的概率
(2)由第(1)问得到第二问的分布列
解答 解:(1)X的可能取值为0,1,2,3
P(X=0)=$\frac{1}{2}×\frac{2}{3}×\frac{1}{3}=\frac{1}{9}$
P(X=1)=$\frac{1}{2}×\frac{2}{3}×\frac{1}{3}+\frac{1}{2}×\frac{1}{3}×\frac{1}{3}+\frac{1}{2}×\frac{2}{3}×\frac{2}{3}=\frac{7}{18}$
P(X=2)=$\frac{1}{2}×\frac{1}{3}×\frac{1}{3}+\frac{1}{2}×\frac{1}{3}×\frac{2}{3}+\frac{1}{2}×\frac{2}{3}×\frac{2}{3}=\frac{7}{18}$
P(X=3)=$\frac{1}{2}×\frac{1}{3}×\frac{2}{3}=\frac{1}{9}$
该高中获得冠军个数X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{9}$ | $\frac{7}{18}$ | $\frac{7}{18}$ | $\frac{1}{9}$ |
| η | 6 | 9 | 12 | 15 |
| P | $\frac{1}{9}$ | $\frac{7}{18}$ | $\frac{7}{18}$ | $\frac{1}{9}$ |
点评 本题主要考查离散型随机变量的分布列,属简单题型,高考时有涉及.


科目:高中数学 来源: 题型:填空题
 将一批工件的尺寸在(40~100mm之间)分成六段,即[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为0.03.
将一批工件的尺寸在(40~100mm之间)分成六段,即[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为0.03.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
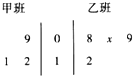 如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.
如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知某几何体的三视图如图所示,其中正视图、侧视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体体积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体体积为( )| A. | $\frac{4\sqrt{2}π}{3}$+$\frac{4}{3}$ | B. | $\frac{8\sqrt{2}π}{3}$+$\frac{4}{3}$ | C. | $\frac{4\sqrt{2}π}{3}$+2 | D. | $\frac{8\sqrt{2}π}{3}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com