
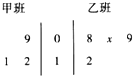
 如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.
如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.分析 (Ⅰ)当x=7时,由茎叶图可知,乙组同学的植树棵数是:7,8,9,10,11,求得中位数,平均数,再根据方差公式求得s2的值.
(Ⅱ)记甲班3名同学为a9,a11,a12,乙班4名同学即为b8,b9,B9,b12,列举出从实践次数大于8的同学中任选两名同学的基本事件,再找到满足两名同学分别在甲、乙两个班级且实践次数的和大于20的基本事件,根据概率公式计算即可.
解答 解:(Ⅰ)当x=7时,由茎叶图可知,乙组同学的植树棵数是:7,8,9,12,
所以已组的中位数为$\frac{8+9}{2}$=8.5,
所以平均数为$\frac{1}{4}$(7+8+9+12)=9,)
方差为s2=$\frac{1}{4}$[(7-9)2+(8-9)2+(9-9)2+(12-9)2]=3.5;
(Ⅱ)记甲班3名同学为a9,a11,a12,乙班4名同学即为b8,b9,B9,b12,从实践次数大于8的同学中任选两名同学,基本事件有a9a11,a9a12,a9b9,a9B9,a9b12,
a11a12,a11b9,a11B9,a11b12,a12b9,a12B9,a12b12,b9B9,b9b12,B9b12,共15个,
选出的两名同学分别在甲、乙两个班级且实践次数的和大于20的基本事件有a9b12,a11b12,a12b9,a12B9,a12b12,共5个,
故选出的两名同学分别在甲、乙两个班级且实践次数的和大于20的概率p=$\frac{5}{15}$=$\frac{1}{3}$.
点评 本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于基础题


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{65}{81}$ | B. | $\frac{19}{27}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 23 | C. | 28 | D. | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{17}}}{3}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{33}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | -6 | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
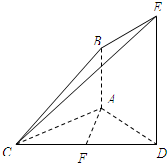 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com