
| A. | 21 | B. | 23 | C. | 28 | D. | 31 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{{\begin{array}{l}{x-y+2≥0}\\{x+y-4≤0}\\{x-3y+3≤0}\end{array}}\right.$作出可行域如图,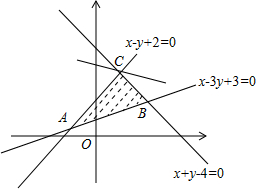
联立$\left\{\begin{array}{l}{x-y+2=0}\\{x+y-4=0}\end{array}\right.$,解得C(1,3),
化目标函数z=4x+8y为$y=-\frac{1}{2}x+\frac{z}{8}$,
由图可知,当直线$y=-\frac{1}{2}x+\frac{z}{8}$过C时,直线在y轴上的截距最大,z有最大值为4×1+3×8=28.
故选:C.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
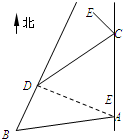 如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | B. | (-∞,-$\frac{\sqrt{3}}{3}$]∪[$\frac{\sqrt{3}}{3}$,+∞) | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $({-∞,-\sqrt{3}}]∪[{\sqrt{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将一批工件的尺寸在(40~100mm之间)分成六段,即[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为0.03.
将一批工件的尺寸在(40~100mm之间)分成六段,即[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为0.03.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
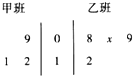 如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.
如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com