
| A. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | B. | (-∞,-$\frac{\sqrt{3}}{3}$]∪[$\frac{\sqrt{3}}{3}$,+∞) | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $({-∞,-\sqrt{3}}]∪[{\sqrt{3},+∞})$ |
分析 用代数法,先联立方程,消元后得到一个方程,再考虑二次项系数为0与不为0讨论,即可求得直线l的斜率的取值范围
解答 解:设直线方程为y=kx-2k
根据题意:$\left\{\begin{array}{l}y=kx-2k\\{x}^{2}+{y}^{2}=1\end{array}\right.$消去y整理得(1+k2)x2-4k2x+4k2-1=0,
因为1+k2≠0,∴△≥0,16k4-4(1+k2)(4k2-1)≥0,
∴k∈[-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$].
故选:A.
点评 本题的考点是直线与圆锥曲线的关系,主要考查直线与双曲线的位置关系,在只有一个公共点时,不要忽视了与渐近线平行的情况.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
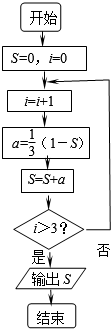
| A. | $\frac{65}{81}$ | B. | $\frac{19}{27}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | 23 | C. | 28 | D. | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com