练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．设向量$\overrightarrow a=（1，-2）$，$\overrightarrow b=（3，4）$，则向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为-1．

    分析 根据投影的定义，应用公式向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为|$\overrightarrow{a}$|cos＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\left|\overrightarrow{b}\right|}$求解．

    解答 解：向量$\overrightarrow a=（1，-2）$，$\overrightarrow b=（3，4）$，根据投影的定义可得：
    向量$\overrightarrow a$在向量$\overrightarrow b$方向上的投影为|$\overrightarrow{a}$|cos＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\left|\overrightarrow{b}\right|}$=$\frac{3-8}{\sqrt{9+16}}$=-1．
    故答案为：-1．

    点评 本题主要考查向量投影的定义及求解的方法，公式与定义两者要灵活运用．解答关键在于要求熟练应用公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．已知点A（-1，5）和向量$\overrightarrow a$=（2，3），若$\overrightarrow{AB}$=3$\overrightarrow{a}$，则点B的坐标为（5，14）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若定义在R上的函数满足f（-x）=f（x），f（4-x）=f（x），且当x∈[0，2]时，f（x）=$\sqrt{4-{x^2}}$，则函数H（x）=|xex|-f（x）在区间[-6，2]上的零点个数为（　　）
    A．2B．4C．6D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若过点（2，0）的直线l与圆C：x2+y2=1有公共点，则直线l的斜率k的取值范围是（　　）
    A．[-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$]B．（-∞，-$\frac{\sqrt{3}}{3}$]∪[$\frac{\sqrt{3}}{3}$，+∞）C．$[{-\sqrt{3}，\sqrt{3}}]$D．$（{-∞，-\sqrt{3}}]∪[{\sqrt{3}，+∞}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

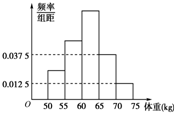    15．为了了解某县今年高考准备报考体育专业的学生的体重情况，将所得的学生体重数据分组整理后，画出了频率分布直方图（如图），已知图中从左到右的前3小组的频率a，b，c恰成等差数列，若抽取的学生人数是48，则第2小组的频数为（　　）
    A．6B．12C．18D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．将一批工件的尺寸在（40～100mm之间）分成六段，即[40，50），[50，60），…，[90，100），得到如图的频率分布直方图，则图中实数a的值为0.03．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知b为实数，i为虚数单位，若$\frac{2+bi}{1-i}$为实数，则b=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F也是抛物线C2：y2=2px（p＞0）的焦点，C1与C2的一个交点为P，若PF⊥x轴，则双曲线C1的离心率为（　　）
    A．$\sqrt{2}$+1B．2$\sqrt{2}$C．2$\sqrt{2}$-1D．$\sqrt{3}$+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{6}$=1与抛物线y2=2px有公共焦点F，双曲线与抛物线的准线交于M、N两点，且△MNF为等边三角形，则p的值为（　　）
    A．2B．2$\sqrt{2}$C．4$\sqrt{2}$D．6

    查看答案和解析>>

    同步练习册答案