
���� �����ݷֲ�����Ķ��尴�ձ�����ȡ���ɣ�
�����衰��ƹ����ӳ�ȡ�Ķ�Ա��������1��Ů��Ա��Ϊ�¼�A�����ó����ηֲ���ø���
����д����������ε�������������ݳ����ηֲ�д�����Ը�����÷ֲ���������
��� ����С������13�֣�
�⣺����ȡƹ�����Ա������Ϊ$3��\frac{10}{15}=2$�ˣ�
��ë���Ա������Ϊ$3��\frac{5}{15}=1$�ˣ���..��2�֣�
�����衰��ƹ����ӳ�ȡ�Ķ�Ա��������1��Ů��Ա��Ϊ�¼�A��
��$P��A��=\frac{C_6^1C_4^1+C_4^2}{{C_{10}^2}}=\frac{2}{3}$��
���Դ�ƹ����ӳ�ȡ�Ķ�Ա��������1��Ů��Ա�ĸ���Ϊ$\frac{2}{3}$����..��6�֣�
����=0��1��2��3
P����=0��=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{10}^{2}{C}_{5}^{1}}=\frac{4}{75}$
P����=1��=$\frac{{C}_{6}^{1}{C}_{4}^{1}{C}_{2}^{1}}{{C}_{10}^{2}{C}_{5}^{1}}+\frac{{C}_{4}^{2}{C}_{3}^{1}}{{C}_{10}^{2}{C}_{5}^{1}}=\frac{22}{75}$
P����=2��=$\frac{{C}_{6}^{2}{C}_{2}^{1}}{{C}_{10}^{2}{C}_{5}^{1}}+\frac{{C}_{6}^{1}{C}_{4}^{1}{C}_{3}^{1}}{{C}_{10}^{2}{C}_{5}^{1}}=\frac{34}{75}$��
P����=3��=$\frac{C_6^2•C_3^1}{{C_{10}^2•C_5^1}}=\frac{1}{5}$��
�εķֲ���Ϊ
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{4}{75}$ | $\frac{22}{75}$ | $\frac{34}{75}$ | $\frac{1}{5}$ |
���� ������Ҫ���鳬���ηֲ���Ӧ�ú���������ķֲ������������е����ͣ��߿��������ͣ�


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ƽ��$\frac{��}{12}$����λ | B�� | ����ƽ��$\frac{��}{6}$����λ | ||
| C�� | ����ƽ��$\frac{��}{12}$����λ | D�� | ����ƽ��$\frac{��}{6}$����λ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{10}$��x1x2��$\frac{1}{e}$ | B�� | $\frac{1}{e}$��x1x2��1 | C�� | 1��x1x2��e | D�� | x1x2��e |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{\sqrt{3}}{3}$��$\frac{\sqrt{3}}{3}$] | B�� | ��-�ޣ�-$\frac{\sqrt{3}}{3}$]��[$\frac{\sqrt{3}}{3}$��+�ޣ� | C�� | $[{-\sqrt{3}��\sqrt{3}}]$ | D�� | $��{-�ޣ�-\sqrt{3}}]��[{\sqrt{3}��+��}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
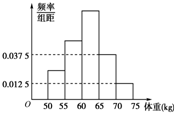 Ϊ���˽�ij�ؽ���߿�����������רҵ��ѧ������������������õ�ѧ���������ݷ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3С���Ƶ��a��b��cǡ�ɵȲ����У�����ȡ��ѧ��������48�����2С���Ƶ��Ϊ��������
Ϊ���˽�ij�ؽ���߿�����������רҵ��ѧ������������������õ�ѧ���������ݷ�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3С���Ƶ��a��b��cǡ�ɵȲ����У�����ȡ��ѧ��������48�����2С���Ƶ��Ϊ��������| A�� | 6 | B�� | 12 | C�� | 18 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com