
| A. | $\frac{65}{81}$ | B. | $\frac{19}{27}$ | C. | $\frac{5}{9}$ | D. | $\frac{1}{3}$ |
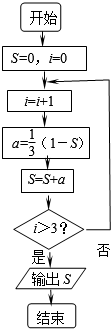
分析 模拟执行程序框图,依次写出每次循环得到的i,a,S的值,当i=4时满足条件i>3,退出循环,输出S的值为$\frac{65}{81}$.
解答 解:模拟执行程序框图,可得
S=0,i=0
i=1
a=$\frac{1}{3}$,S=$\frac{1}{3}$,
不满足条件i>3,i=2,a=$\frac{2}{9}$,S=$\frac{5}{9}$
不满足条件i>3,i=3,a=$\frac{4}{27}$,S=$\frac{19}{27}$
不满足条件i>3,i=4,a=$\frac{8}{81}$,S=$\frac{65}{81}$
满足条件i>3,退出循环,输出S的值为$\frac{65}{81}$.
故选:A.
点评 本题主要考查了循环结构的程序框图,正确依次写出每次循环得到的i,a,S的值是解题的关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
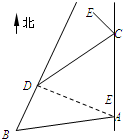 如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向用与B相距10$\sqrt{2}$ 海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | B. | (-∞,-$\frac{\sqrt{3}}{3}$]∪[$\frac{\sqrt{3}}{3}$,+∞) | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $({-∞,-\sqrt{3}}]∪[{\sqrt{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将一批工件的尺寸在(40~100mm之间)分成六段,即[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为0.03.
将一批工件的尺寸在(40~100mm之间)分成六段,即[40,50),[50,60),…,[90,100),得到如图的频率分布直方图,则图中实数a的值为0.03.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
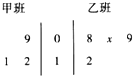 如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.
如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com