
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,直线
,直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() ,求证:若圆
,求证:若圆![]() 与直线
与直线![]() 相切,则圆
相切,则圆![]() 与直线
与直线![]() 也相切.
也相切.
【答案】(I)![]() ;(II)证明见解析.
;(II)证明见解析.
【解析】试题分析:(1)利用条件布列![]() 的方程组,即可得到椭圆
的方程组,即可得到椭圆![]() 的标准方程;(2)对直线l的斜率分类讨论,若圆
的标准方程;(2)对直线l的斜率分类讨论,若圆![]() 与直线
与直线![]() 相切,则圆
相切,则圆![]() 与直线
与直线![]() 也相切等价于
也相切等价于
![]() ,联立方程,借助根与系数关系证明等式即可.
,联立方程,借助根与系数关系证明等式即可.
试题解析:
(Ⅰ)设椭圆C的焦距为2c(c>0),依题意, 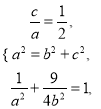
解得![]() ,c=1,故椭圆C的标准方程为
,c=1,故椭圆C的标准方程为![]() ;
;
(Ⅱ)证明:当直线l的斜率不存在时,直线l的方程为![]() ,M,N两点关于x轴对称,点P(4,0)在x轴上,所以直线PM与直线PN关于x轴对称,所以点O到直线PM与直线PN的距离相等,故若圆
,M,N两点关于x轴对称,点P(4,0)在x轴上,所以直线PM与直线PN关于x轴对称,所以点O到直线PM与直线PN的距离相等,故若圆![]() 与直线PM相切,则也会与直线PN相切;
与直线PM相切,则也会与直线PN相切;
当直线l的斜率存在时,设直线l的方程为![]() ,
, ![]() ,
, ![]() ,
,
由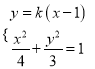 得:
得: ![]()
所以![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
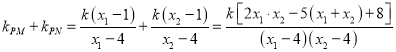
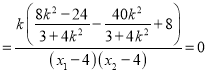 ,
,
所以, ![]() ,于是点O到直线PM与直线的距离PN相等,
,于是点O到直线PM与直线的距离PN相等,
故若圆![]() 与直线PM相切,则也会与直线PN相切;
与直线PM相切,则也会与直线PN相切;
综上所述,若圆![]() 与直线PM相切,则圆
与直线PM相切,则圆![]() 与直线PN也相切.
与直线PN也相切.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 是等边三角形.
是等边三角形.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与线段
与线段![]() 交于点
交于点![]() ,若
,若![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,a2=![]() ,an+1-
,an+1-![]() an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
an+an-1=0 (n≥2,且n∈N*),若数列{an+1+λan}是等比数列.
(1)求实数λ;
(2)求数列{an}的通项公式;
(3)设![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为![]() 的正方形
的正方形![]() (及其内部)绕
(及其内部)绕![]() 旋转一周形成圆柱,如图,
旋转一周形成圆柱,如图, ![]() 长为
长为![]() ,
, ![]() 长为
长为![]() ,其中
,其中![]() 与
与![]() 在平面
在平面![]() 的同侧.
的同侧.
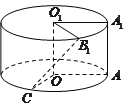
(1)求三棱锥![]() 的体积;
的体积;
(2)求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
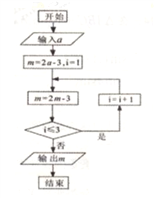
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该著作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,对我国民间普及珠算和数学知识起到了很大的作用,如图所示的程序框图的算法思路源于该著作中的“李白沽酒”问题,执行该程序框图,若输出的![]() 的值为0,则输入的
的值为0,则输入的![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com