
| A. | (1,$\sqrt{2}$) | B. | (1,$\sqrt{3}$+1) | C. | ($\sqrt{2}$,+∞) | D. | ($\sqrt{2}$,$\sqrt{3}$+1) |
分析 设F'为双曲线的左焦点,连接AF',BF',由$\overrightarrow{AF}$•$\overrightarrow{BF}$=0,可得AF⊥BF,可得四边形AFBF'为矩形,可设AF=m,BF=n,由双曲线的定义可得m-n=2a,m2+n2=4c2,解得m,n,在直角三角形ABF中,tan∠BAF=$\frac{BF}{AF}$,由正切函数值,解不等式,结合离心率公式,即可得到所求范围.
解答 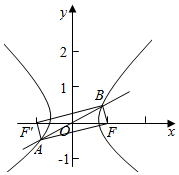 解:设F'为双曲线的左焦点,连接AF',BF',
解:设F'为双曲线的左焦点,连接AF',BF',
由$\overrightarrow{AF}$•$\overrightarrow{BF}$=0,可得AF⊥BF,
可得四边形AFBF'为矩形,
可设AF=m,BF=n,
由双曲线的定义可得m-n=2a,m2+n2=4c2,
由c2=a2+b2,
解得m=$\sqrt{2{b}^{2}+{a}^{2}}$+a,n=$\sqrt{2{b}^{2}+{a}^{2}}$-a,
在直角三角形ABF中,tan∠BAF=$\frac{BF}{AF}$=$\frac{\sqrt{2{b}^{2}+{a}^{2}}-a}{\sqrt{2{b}^{2}+{a}^{2}}+a}$,
由∠BAF∈($\frac{π}{12}$,$\frac{π}{6}$),可得2-$\sqrt{3}$<$\frac{\sqrt{2{b}^{2}+{a}^{2}}-a}{\sqrt{2{b}^{2}+{a}^{2}}+a}$<$\frac{\sqrt{3}}{3}$,
化简可得($\sqrt{3}$-1)$\sqrt{2{b}^{2}+{a}^{2}}$>(3-$\sqrt{3}$)a,
即有b2>a2,即c2>2a2,即有e>$\sqrt{2}$,
又($\sqrt{3}$-1)$\sqrt{2{b}^{2}+{a}^{2}}$>(1+$\sqrt{3}$)a,
可得b2<(3+2$\sqrt{3}$)a2,即有c2<(4+2$\sqrt{3}$)a2,
可得e<1+$\sqrt{3}$,
综上可得,e的范围是($\sqrt{2}$,1+$\sqrt{3}$).
故选:D.
点评 本题考查双曲线的离心率的范围,考查双曲线的定义和勾股定理的运用,考查锐角的正切函数的运用,以及化简整理的运算能力,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
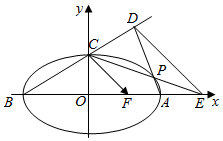 如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.
如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线l平行于直线m | B. | 直线l与直线m异面 | ||
| C. | 直线l与直线m没有公共点 | D. | 直线l与直线m不垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com