
分析 (1)根据根式函数以及一元二次函数的性质即可求f(x)的值域;
(2)若点(3,2)到函数g(x)图象所表示的直线的距离为3,利用点到直线的距离关系进行求解即可求a值;
(3)利用数形结合转化为直线和圆的位置关系即可得到结论.
解答 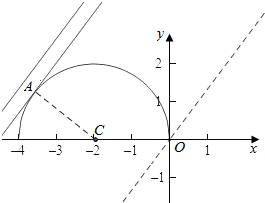 解:(1)由-x2-4x≥0得x2+4x≤0,即-4≤x≤0,
解:(1)由-x2-4x≥0得x2+4x≤0,即-4≤x≤0,
此时f(x)=$\sqrt{-{x}^{2}-4x}$=$\sqrt{-(x+2)^{2}+4}$∈[0,2],即函数f(x)的值域为[0,2].
(2)由g(x)=$\frac{4}{3}$x+1-a=y得4x-3y+3(1-a)=0,
则若点(3,2)到函数g(x)图象所表示的直线的距离为3,
则d=$\frac{|4×3-3×2+3(1-a)|}{\sqrt{{3}^{2}+{4}^{2}}}$=3,
即$\frac{|12-6+3-3a|}{5}=\frac{|9-3a|}{5}=3$,
则|3-a|=5,即a=8或a=-2.
(3)若有f(x)≤g(x)恒成立,
则函数f(x)对应的图象,在g(x)的图象下方,
函数f(x)=$\sqrt{-{x}^{2}-4x}$,表示以C(-2,0)为圆心,半径r=2的圆的上半部分,
则直线g(x)=$\frac{4}{3}$x+1-a的截距1-a>0,即a<1,
则满足圆心C到直线4x-3y+3(1-a)=0的距离d≥2,
即$\frac{|-2×4+3-3a|}{\sqrt{{3}^{2}+{4}^{2}}}=\frac{|3a+5|}{5}$≥2,
则|3a+5|≥10,
即3a+5≥10或3a+5≤-10,
即3a≥5或3a≤-15,
即a≥$\frac{5}{3}$(舍)或a≤-5,
即实数a的取值范围是(-∞,-5].
点评 本题主要考查函数值域以及点到直线的距离的计算,不等式恒成立问题,利用数形结合进行转化是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{15}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
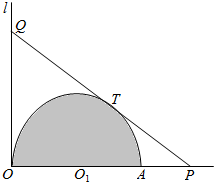 如图,阴影部分为古建筑物保护群所在地,其形状是以O1为圆心,半径为1km的半圆面.公路l经过点O,且与直径OA垂直,现计划修建一条与半圆相切的公路PQ(点P在直径OA的延长线上,点Q在公路l上),T为切点.
如图,阴影部分为古建筑物保护群所在地,其形状是以O1为圆心,半径为1km的半圆面.公路l经过点O,且与直径OA垂直,现计划修建一条与半圆相切的公路PQ(点P在直径OA的延长线上,点Q在公路l上),T为切点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,1) | B. | ($\frac{2}{3}$,+∞) | C. | (0,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+1 | B. | y=2cosx | C. | y=-$\frac{1}{x}$ | D. | y=x|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com