
分析 (Ⅰ)利用2010年该地区人口共计105万求W的值,利用$\frac{142}{1+0.35×(0.94)^{x-2010}}$≥142,即可判断未来该地区的人口总数是否有可能突破142万;
(Ⅱ)利用该地区2013年恰好进入老龄化社会,求出k%≈$\frac{1}{30}$,即可预测2040年该地区60岁以上人口数.
解答 解:(Ⅰ)∵2010年该地区人口共计105万,
∴x=2010,P=$\frac{W}{1+0.35}$=105,
∴W≈142.
令$\frac{142}{1+0.35×(0.94)^{x-2010}}$≥142,
∴0.35×(0.94)x-2010≤0无解,
∴未来该地区的人口总数不可能突破142万;
(Ⅰ)∵该地区2013年恰好进入老龄化社会,
∴10×[1+k%•(2013-2010)]=10%×$\frac{142}{1+0.35×0.9{4}^{3}}$,
∴k%≈$\frac{1}{30}$,
∴x=2040,L(2040)≈10×[1+$\frac{1}{30}$•(2040-2010)]=20万
点评 本题考查利用数学知识解决实际问题,考查学生的计算能力,正确理解题意是关键.


科目:高中数学 来源: 题型:选择题
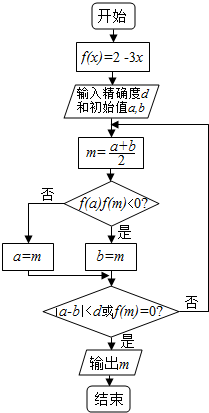 阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )
阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )| x | f(x)=2x-3x |
| 0.25 | 0.44 |
| 0.375 | 0.17 |
| 0.4375 | 0.04 |
| 0.46875 | -0.02 |
| 0.5 | -0.08 |
| A. | 0.375 | B. | 0.4375 | C. | 0.46875 | D. | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com