
分析 根据函数的奇偶性和对称性进行求解即可.
解答 解:∵f(x)是R上的偶函数,0≤φ≤π,
∴φ=$\frac{π}{2}$,
则f(x)=sin(ωx+$\frac{π}{2}$)=cosωx,
∵f(x)图象关于点M($\frac{3}{4}$π,0)对称,
∴f($\frac{3}{4}$π)=cos($\frac{3}{4}$πω)=0,
即$\frac{3}{4}$πω=$\frac{π}{2}$+kπ,k∈Z,
即ω=$\frac{2}{3}$+$\frac{4}{3}$k,k∈Z,
∵f(x)在区间[0,π]上是单调函数,
∴$\frac{T}{2}≥π$,即$\frac{π}{ω}≥π$,
∴0<ω≤1,
即当k=0时,ω=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$,$\frac{π}{2}$.
点评 本题主要考查三角函数解析式的求解,根据三角函数的单调性和奇偶性和对称性是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
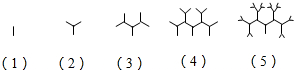 如图所示是按照一定规律画出的一列“树型”图,设第n个图有an个“树枝”,则an+1与an(n≥1)之间的关系是an+1=2an+1(n≥1).
如图所示是按照一定规律画出的一列“树型”图,设第n个图有an个“树枝”,则an+1与an(n≥1)之间的关系是an+1=2an+1(n≥1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>d,则ab>cd | B. | 若|a|<b,则a+b>0 | ||
| C. | 若a>b>0,则ab>ba | D. | 若$\frac{1}{a}>\frac{1}{b}$,则a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 接受挑战 | 不接受挑战 | 合计 | |
| 男性 | 50 | 10 | 60 |
| 女性 | 25 | 15 | 40 |
| 合计 | 75 | 25 | 100 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com