
分析 根据题意和奇函数的定义判断出h(x)的奇偶性,由函数单调性的定义判断出h(x)的单调性,结合条件画出函数图象的示意图,由图象求出不等式的解集.
解答 解:∵f(x)、g(x)分别是定义在R上的奇函数和偶函数,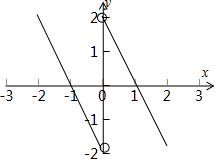
∴h(x)=f(x)g(x)是R上的奇函数,
∵任意x1,x2∈(0,+∞),都有$\frac{h({x}_{1})-h({x}_{2})}{{x}_{1}-{x}_{2}}$<0,
∴h(x)在(0,+∞)上为减函数,
则h(x)在(-∞,0)上也为减函数,
又g(1)=0,∴h(1)=f(1)g(1)=0,且h(-1)=0,
画出函数h(x)的图象示意图:
∴不等式x•h(x)<0的解集是(-∞,-1)∪(1,+∞),
故答案为:(-∞,-1)∪(1,+∞).
点评 本题考查函数的奇偶性与单调性的综合应用,考查数形结合思想,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{n(n+1)}{2}$ | B. | $\frac{2n}{n+1}$ | C. | $\frac{2}{n(n+1)}$ | D. | $\frac{n}{n+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.
在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=AA1=2,D、E分别为棱AB、BC的中点,点F在棱AA1上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 504 | B. | 600 | C. | 720 | D. | 1000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com