
如图,椭圆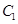 与椭圆
与椭圆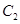 中心在原点,焦点均在
中心在原点,焦点均在 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆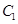 的长轴长为
的长轴长为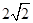 ,且椭圆
,且椭圆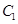 的左准线
的左准线 被椭圆
被椭圆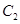 截得的线段
截得的线段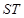 长为
长为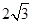 ,已知点
,已知点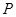 是椭圆
是椭圆 上的一个动点.
上的一个动点.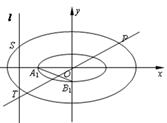
⑴求椭圆 与椭圆
与椭圆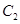 的方程;
的方程;
⑵设点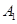 为椭圆
为椭圆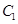 的左顶点,点
的左顶点,点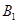 为椭圆
为椭圆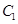 的下顶点,若直线
的下顶点,若直线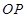 刚好平分
刚好平分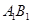 ,求点
,求点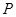 的坐标;
的坐标;
⑶若点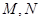 在椭圆
在椭圆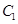 上,点
上,点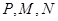 满足
满足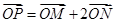 ,则直线
,则直线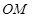 与直线
与直线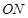 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
(1)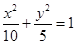 ,(2)
,(2)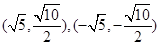 ,(3)
,(3)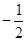 .
.
解析试题分析:(1)求椭圆方程,基本方法是待定系数法.关键是找全所需条件. 椭圆中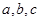 三个未知数的确定只需两个独立条件,根据椭圆
三个未知数的确定只需两个独立条件,根据椭圆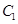 的长轴长为
的长轴长为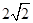 得
得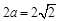 ,又由椭圆
,又由椭圆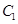 的左准线
的左准线 得
得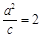 ,所以
,所以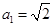 ,
,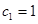 ,
,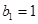 ,就可得到椭圆
,就可得到椭圆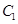 的标准方程;由椭圆
的标准方程;由椭圆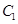 与椭圆
与椭圆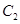 离心率相同,得
离心率相同,得 再由椭圆
再由椭圆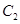 过点
过点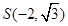 ,代入可得椭圆
,代入可得椭圆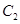
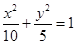 (2)涉及弦中点问题,一般用“点差法”构造等量关系.本题较简单,可直接求出
(2)涉及弦中点问题,一般用“点差法”构造等量关系.本题较简单,可直接求出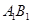 中点坐标,再利用直线
中点坐标,再利用直线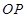 与椭圆
与椭圆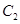 联立方程组求交点坐标;(3)求定值问题,一是确定定值,这可利用特殊情况給于确定,二是参数选择,不仅要揭示问题本质,更要易于消元,特别是整体消元.本题研究的是直线
联立方程组求交点坐标;(3)求定值问题,一是确定定值,这可利用特殊情况給于确定,二是参数选择,不仅要揭示问题本质,更要易于消元,特别是整体消元.本题研究的是直线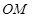 与直线
与直线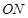 的斜率之积,即它们坐标满足
的斜率之积,即它们坐标满足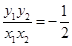 为定值,参数选为点
为定值,参数选为点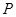 的坐标,利用点
的坐标,利用点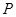 的坐标满足
的坐标满足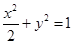 进行整体消元.
进行整体消元.
试题解析:⑴设椭圆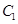 方程为
方程为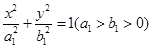 ,椭圆
,椭圆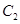 方程为
方程为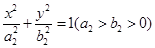 ,
,
则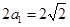 ,∴
,∴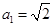 ,又其左准线
,又其左准线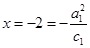 ,∴
,∴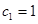 ,则
,则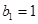
∴椭圆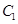 方程为
方程为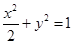 ,其离心率为
,其离心率为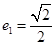 , 3分
, 3分
∴椭圆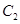 中
中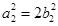 ,由线段的
,由线段的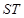 长为
长为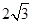 ,得
,得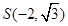 ,代入椭圆
,代入椭圆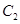
 ,
,
得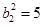 ,∴
,∴ ,椭圆
,椭圆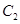 方程为
方程为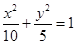 ; 6分
; 6分
⑵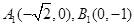 ,则
,则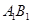 中点为
中点为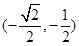 ,∴直线
,∴直线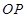 为
为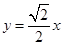 , 7分
, 7分
由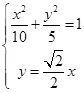 ,得
,得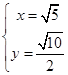 或
或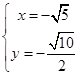 ,
,
∴点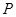 的坐标为
的坐标为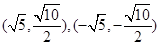 ; 10分
; 10分
⑶设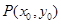 ,
,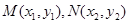 ,则
,则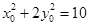 ,
,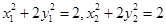 ,
,
由题意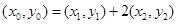 ,∴
,∴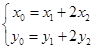 12分
12分
∴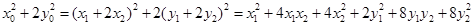
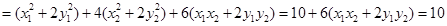 14分
14分
∴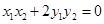


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
已知椭圆C1: +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上, =2
=2 ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: =1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+
=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+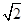 =0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
=0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
(1)求椭圆C的方程;
(2)设M是椭圆的上顶点,过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1,k2,且k1+k2=4,证明:直线AB过定点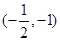 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于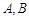 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,求
能否垂直?若能,求 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求
,求 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知抛物线的顶点在坐标原点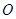 ,焦点
,焦点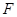 在
在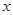 轴上,抛物线上的点
轴上,抛物线上的点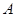 到
到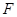 的距离为2,且
的距离为2,且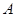 的横坐标为1.直线
的横坐标为1.直线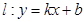 与抛物线交于
与抛物线交于 ,
, 两点.
两点.
(1)求抛物线的方程;
(2)当直线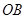 ,
,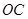 的倾斜角之和为
的倾斜角之和为 时,证明直线
时,证明直线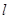 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系中,已知点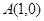 ,点
,点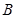 在直线
在直线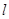 :
: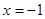 上运动,过点
上运动,过点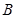 与
与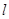 垂直的直线和线段
垂直的直线和线段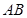 的垂直平分线相交于点
的垂直平分线相交于点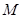 .
.
(1)求动点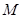 的轨迹
的轨迹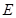 的方程;
的方程;
(2)过(1)中的轨迹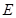 上的定点
上的定点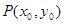
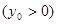 作两条直线分别与轨迹
作两条直线分别与轨迹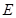 相交于
相交于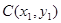 ,
,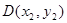 两点.试探究:当直线
两点.试探究:当直线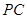 ,
,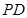 的斜率存在且倾斜角互补时,直线
的斜率存在且倾斜角互补时,直线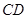 的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
的斜率是否为定值?若是,求出这个定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线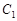 的极坐标方程为
的极坐标方程为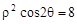 ,曲线
,曲线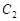 的极坐标方程为
的极坐标方程为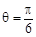 ,曲线
,曲线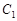 、
、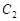 相交于
相交于 、
、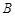 两点.(
两点.(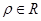 )
)
(Ⅰ)求 、
、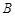 两点的极坐标;
两点的极坐标;
(Ⅱ)曲线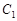 与直线
与直线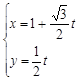 (
(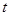 为参数)分别相交于
为参数)分别相交于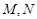 两点,求线段
两点,求线段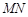 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com