
分析 (Ⅰ)根据正弦定理、两角和的正弦公式化简已知的式子,由A的范围和特殊角的三角函数值求出A;
(Ⅱ)由三角形的面积公式和余弦定理列出方程,化简后把$\frac{b}{c}$作为一个整体求解即可.
解答 解:(Ⅰ)∵atanA-ccosB=bcosC,
∴由正弦定理得,sinAtanA-sinCccosB=sinBcosC,
sinAtanA=sinCccosB+sinBcosC=sin(B+C),
∵B+C=π-A,∴sin(B+C)=sinA,则sinAtanA=sinA,
又sinA≠0,则tanA=1,
由0<A<π得,A=$\frac{π}{4}$;
(Ⅱ)又sinA≠0,则tanA=1,
由0<A<π得,A=$\frac{π}{4}$;
(Ⅱ)∵AD是BC边上的高,且$AD=\frac{1}{2}a$,
∴△ABC的面积S=$\frac{1}{2}×a×\frac{1}{2}a=\frac{1}{2}bcsinA$,则${a}^{2}=\sqrt{2}bc$,
由余弦定理得,a2=b2+c2-2bccosA,
化简得${b}^{2}+{c}^{2}-2\sqrt{2}bc=0$,
两边同除c2可得,$(\frac{b}{c})^{2}-2\sqrt{2}•\frac{b}{c}+1=0$,
解得$\frac{b}{c}=\sqrt{2}±1$.
点评 本题考查正弦定理、余弦定理,两角和的正弦公式,考查化简、变形能力,属于中档题.


科目:高中数学 来源: 题型:选择题
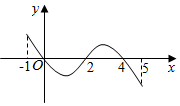 已知函数f(x)的定义域为[-1,5],部分对应值如表.f(x)的导函数y=f'(x)的图象如图所示.下列四个命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表.f(x)的导函数y=f'(x)的图象如图所示.下列四个命题:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4e}{e+1}$ | B. | $\frac{4}{e+1}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则$\overline{AM}•\overline{DC}$的最大值是( )
如图,已知:|AC|=|BC|=4,∠ACB=90°,M为BC的中点,D为以AC为直径的圆上一动点,则$\overline{AM}•\overline{DC}$的最大值是( )| A. | $8+4\sqrt{5}$ | B. | $8-4\sqrt{5}$ | C. | $4+8\sqrt{5}$ | D. | $8\sqrt{5}-4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$) | C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)∥($\overrightarrow{a}$-$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com