
| A. | $\frac{17}{2}$ | B. | $\sqrt{11}$ | C. | $\sqrt{6}$ | D. | 6 |
分析 可根据条件画出图形,根据向量加法的几何意义有$\overrightarrow{AC′}=\overrightarrow{AA′}+\overrightarrow{A′B′}+\overrightarrow{A′D′}$,这样由条件便可进行数量积的运算求出${\overrightarrow{AC′}}^{2}$的值,即求出$|\overrightarrow{AC′}|$的值,从而得到AC′的值.
解答 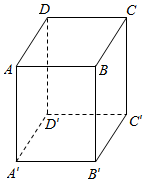 解:如图,根据条件:
解:如图,根据条件:
$|\overrightarrow{AC′}{|}^{2}=|\overrightarrow{AA′}+\overrightarrow{A′B′}+\overrightarrow{B′C′}{|}^{2}$
=$|\overrightarrow{AA′}+\overrightarrow{A′B′}+\overrightarrow{A′D′}{|}^{2}$
=${\overrightarrow{AA′}}^{2}+{\overrightarrow{A′B′}}^{2}+{\overrightarrow{A′D′}}^{2}+2\overrightarrow{AA′}•\overrightarrow{A′B′}$$+2\overrightarrow{AA′}•\overrightarrow{A′D′}+2\overrightarrow{A′B′}•\overrightarrow{A′D′}$
=4+1+1+2+2+1
=11
∴$|\overrightarrow{AC′}|=\sqrt{11}$
即AC′=$\sqrt{11}$.
故选:B.
点评 考查平行六面体的概念,菱形的概念,以及向量加法的几何意义,相等向量的概念,向量数量积的运算及计算公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
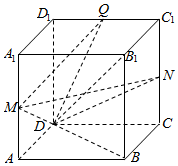 已知四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.
已知四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
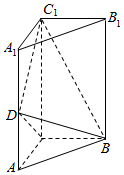 如图,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=$\frac{1}{2}A{A_1}$,D是棱AA1的中点,DC1⊥BD.
如图,三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=BC=$\frac{1}{2}A{A_1}$,D是棱AA1的中点,DC1⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.过点E的平面α垂直于平面SAC.
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.过点E的平面α垂直于平面SAC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
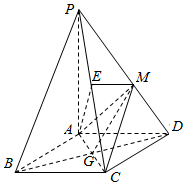 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AD,点M是PD的中点,作ME⊥PC,交PC于点E.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AD,点M是PD的中点,作ME⊥PC,交PC于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29尺 | B. | 24尺 | C. | 26尺 | D. | 30尺 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com