
分析 (1)求得f(x)的导数,求得切线的斜率和切点,解方程可得s,k;
(2)运用分析法证明,即证${e^{a_n}}>{a_n}+1$,令t(x)=ex-x-1(x>0),求得导数,单调性,即可得证;
(3)即讨论$h(x)=g(x)-f(-x)+2={e^x}+\frac{1}{2}{x^3}-ax+1(x>0)$的零点的个数,求得h(x)的导数,求出单调区间和最小值,讨论0<t<1,t=1,t>1,求得h(x)的最小值与0的大小,即可得到零点的个数.
解答 解:(1)由题意得f(0)=0,f′(0)=1,
函数f(x)=s-ke-x的导数为f′(x)=ke-x,
则$\left\{\begin{array}{l}s-k=0\\ k=1\end{array}\right.$,
解得s=1,k=1;
(2)证明:∵f(x)=1-e-x,正项数列{an}满足${a_1}=\frac{1}{2}$,${a_n}={e^{{a_{n+1}}}}f({a_n})$,
∴${e^{{a_{n+1}}}}=\frac{a_n}{{f({a_n})}}=\frac{a_n}{{1-{e^{-{a_n}}}}}$,
数列{an}是递减数列,
可得an+1<an,
即${e^{{a_{n+1}}}}<{e^{a_n}}$,可得$\frac{a_n}{{1-{e^{-{a_n}}}}}<{e^{a_n}}$,
即有${e^{a_n}}>{a_n}+1$,
令t(x)=ex-x-1(x>0),
∵t'(x)=ex-1>0(x>0)
∴t(x)是(0,+∞)上的增函数,
∴t(x)>t(0)=0,即ex>x+1,
故${e^{a_n}}>{a_n}+1$,
∴{an}是递减数列.
(3)即讨论$h(x)=g(x)-f(-x)+2={e^x}+\frac{1}{2}{x^3}-ax+1(x>0)$的零点的个数,
对h(x)求导得$h'(x)={e^x}+\frac{3}{2}{x^2}-a(x>0)$,
易知h'(x)在(0,+∞)上是增函数,
∵h'(0)=1-a<0,$h'(\sqrt{\frac{2a}{3}})={e^{\sqrt{\frac{2a}{3}}}}>0$,
∴$?t∈(0\;\;,\;\;\sqrt{\frac{2a}{3}})$,使h'(t)=0,即$a={e^t}+\frac{{3{t^2}}}{2}$,
∴h(x)在(0,t)递减,在(t,+∞)递增,
∴h(x)在(0,+∞)上的最小值为h(x)min=(1-t)(et+t2+t+1),
①当0<t<1即$1<a<e+\frac{3}{2}$时,h(x)min>0,
此时h(x)在(0,+∞)内无零点;
②当t=1即$a=e+\frac{3}{2}$时,h(x)min=0,
此时h(x)在(0,+∞)内有一个零点;
③当t>1即$a>e+\frac{3}{2}$时,h(x)min<0,
又 h(0)=2>0,x→+∞时,h(x)→+∞
所以h(x)在(0,+∞)内有两个零点;
综上:当$1<a<e+\frac{3}{2}$时,函数f(-x)-2与g(x)的图象无公共点;
当$a=e+\frac{3}{2}$时,函数f(-x)-2与g(x)的图象有一个公共点;
当$a>e+\frac{3}{2}$时,函数f(-x)-2与g(x)的图象有两个公共点.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查数列的单调性的证明,注意运用构造函数法,求得导数判断单调性,考查两式的大小比较,注意运用构造函数法,求得导数判断单调性,求得最小值,考查分类讨论的思想方法,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | $\sqrt{11}$ | C. | $\sqrt{6}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的体积为( )| A. | $8\sqrt{3}$ | B. | 8 | C. | $\frac{{8\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $ln{x_0}>{x_0}^{\frac{1}{2}}>{2^{x_0}}$ | B. | ${2^{x_0}}>ln{x_0}>{x_0}^{\frac{1}{2}}$ | ||
| C. | ${2^{x_0}}>{x_0}^{\frac{1}{2}}>ln{x_0}$ | D. | ${x_0}^{\frac{1}{2}}>{2^{x_0}}>ln{x_0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
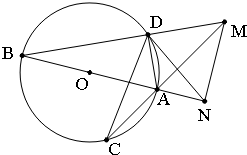 如图,AB是圆O的直径,弦BD、CA的延长线相交于点M,MN垂直BA的延长线于点N.
如图,AB是圆O的直径,弦BD、CA的延长线相交于点M,MN垂直BA的延长线于点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | (1,2] | C. | ($\frac{4}{3}$,2] | D. | ($\frac{1}{3}$,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com