
| A. | $ln{x_0}>{x_0}^{\frac{1}{2}}>{2^{x_0}}$ | B. | ${2^{x_0}}>ln{x_0}>{x_0}^{\frac{1}{2}}$ | ||
| C. | ${2^{x_0}}>{x_0}^{\frac{1}{2}}>ln{x_0}$ | D. | ${x_0}^{\frac{1}{2}}>{2^{x_0}}>ln{x_0}$ |
分析 利用函数零点的定义以及判定定理,求得x0∈(1,2),可得∴${2}^{{x}_{0}}$、$\sqrt{{x}_{0}}$、lnx0 的大小关系.
解答 解:∵函数$f(x)=lnx-\frac{1}{x}$的零点为x0,则x0>0,且lnx0 =$\frac{1}{{x}_{0}}$.
再根据f(x)在(0,+∞)为增函数,f(1)=-1<0,f(2)=ln2-$\frac{1}{2}$>0,f(1)•f(2)<0,
可得x0∈(1,2),${2}^{{x}_{0}}$>2,$\sqrt{{x}_{0}}$∈(1,2),lnx0∈( 0,ln2),
∴${2}^{{x}_{0}}$>$\sqrt{{x}_{0}}$>lnx0,
故选:C.
点评 本题主要考查函数零点的定义以及判定定理,属于基础题.


科目:高中数学 来源: 题型:解答题
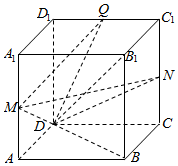 已知四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.
已知四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
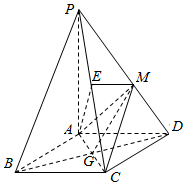 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AD,点M是PD的中点,作ME⊥PC,交PC于点E.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AD,点M是PD的中点,作ME⊥PC,交PC于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
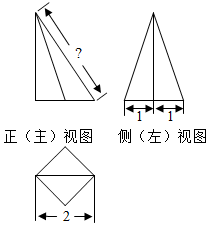 一个底面为正方形的四棱锥,其三视图如图所示,若这个四棱锥的体积为2,则此四棱锥最长的侧棱长为( )
一个底面为正方形的四棱锥,其三视图如图所示,若这个四棱锥的体积为2,则此四棱锥最长的侧棱长为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{11}$ | C. | $\sqrt{13}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,在所有棱长均为1的四面体DEFG内有一个内接三棱柱ABC-A1B1C1,A,B,C在平面EFG内,A1,B1、C1分别在DE,DF,DG上,且AB=BC=CA=AA1,AA1⊥平面ABC,则AB=$\sqrt{6}$-2.
如图所示,在所有棱长均为1的四面体DEFG内有一个内接三棱柱ABC-A1B1C1,A,B,C在平面EFG内,A1,B1、C1分别在DE,DF,DG上,且AB=BC=CA=AA1,AA1⊥平面ABC,则AB=$\sqrt{6}$-2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29尺 | B. | 24尺 | C. | 26尺 | D. | 30尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com