
 如图所示,在所有棱长均为1的四面体DEFG内有一个内接三棱柱ABC-A1B1C1,A,B,C在平面EFG内,A1,B1、C1分别在DE,DF,DG上,且AB=BC=CA=AA1,AA1⊥平面ABC,则AB=$\sqrt{6}$-2.
如图所示,在所有棱长均为1的四面体DEFG内有一个内接三棱柱ABC-A1B1C1,A,B,C在平面EFG内,A1,B1、C1分别在DE,DF,DG上,且AB=BC=CA=AA1,AA1⊥平面ABC,则AB=$\sqrt{6}$-2. 分析 作DO⊥平面EFG,垂足为O,交平面A1B1C1于O1,连接OG,O1C1,利用三角形相似建立方程,即可得出结论.
解答 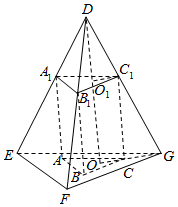 解:作DO⊥平面EFG,垂足为O,交平面A1B1C1于O1,连接OG,O1C1,则OG=$\frac{\sqrt{3}}{3}$,DO=$\sqrt{1-\frac{1}{3}}$=$\frac{\sqrt{6}}{3}$,
解:作DO⊥平面EFG,垂足为O,交平面A1B1C1于O1,连接OG,O1C1,则OG=$\frac{\sqrt{3}}{3}$,DO=$\sqrt{1-\frac{1}{3}}$=$\frac{\sqrt{6}}{3}$,
设AB=a,则由三角形相似可得$\frac{\frac{\sqrt{3}}{3}a}{\frac{\sqrt{3}}{3}}=\frac{\frac{\sqrt{6}}{3}-a}{\frac{\sqrt{6}}{3}}$,
∴a=$\frac{\sqrt{6}}{3+\sqrt{6}}$=$\sqrt{6}$-2.
故答案为:$\sqrt{6}$-2.
点评 本题考查点面距离的计算,考查三角形相似性质的运用,比较基础.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $ln{x_0}>{x_0}^{\frac{1}{2}}>{2^{x_0}}$ | B. | ${2^{x_0}}>ln{x_0}>{x_0}^{\frac{1}{2}}$ | ||
| C. | ${2^{x_0}}>{x_0}^{\frac{1}{2}}>ln{x_0}$ | D. | ${x_0}^{\frac{1}{2}}>{2^{x_0}}>ln{x_0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
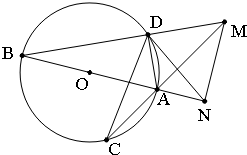 如图,AB是圆O的直径,弦BD、CA的延长线相交于点M,MN垂直BA的延长线于点N.
如图,AB是圆O的直径,弦BD、CA的延长线相交于点M,MN垂直BA的延长线于点N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com