
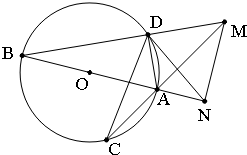
 如图,AB是圆O的直径,弦BD、CA的延长线相交于点M,MN垂直BA的延长线于点N.
如图,AB是圆O的直径,弦BD、CA的延长线相交于点M,MN垂直BA的延长线于点N.分析 (1)由AB是圆O的直径,得∠ADM=90°,又MN垂直BA的延长线于点N,得∠ANM=90°,可得M、N、A、D四点共圆,然后利用等量关系求得∠ADC=∠ADN,
可得DA是∠CDN的角分线;
(2)由M、N、A、D四点共圆,得AB•NB=BM•BD,B、C、A、D四点共圆,得MD•MB=MA•MC,联立可得MD•MB+MB•BD=MA•MC+AB•BN,从而得
得BM2=MA2+AB2+MA•AC+AB•AN,再由B、C、M、N四点共圆,得MA•AC=AB•AN,可得BM2=AB2+AM2+2AB•AN.
解答 证明:(1)∵AB是圆O的直径,∴AD⊥BD,即∠ADM=90°,
又MN垂直BA的延长线于点N,即∠ANM=90°,
∴M、N、A、D四点共圆,
∴∠MDN=∠NAM,
∵∠BAC=∠NAM,∠BAC=∠BDC,∴∠BDC=∠MDN,
又∠ADM=∠ADB=90°,∴∠ADC=∠ADN,
∴DA是∠CDN的角分线;
(2)∵M、N、A、D四点共圆,
∴AB•NB=BM•BD,①
∵B、C、A、D四点共圆,
∴MD•MB=MA•MC,②
①+②有:
MD•MB+MB•BD=MA•MC+AB•BN,
得BM2=MA•(MA+AC)+AB•(AB+AN)=MA2+AB2+MA•AC+AB•AN,
∵B、C、M、N四点共圆,∴MA•AC=AB•AN,
∴BM2=AB2+AM2+2AB•AN.
点评 本题考查与圆有关的比例线段,考查了四点共圆的条件,考查分析问题和解决问题的能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
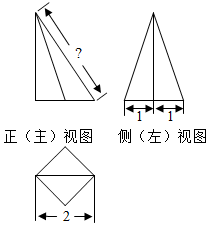 一个底面为正方形的四棱锥,其三视图如图所示,若这个四棱锥的体积为2,则此四棱锥最长的侧棱长为( )
一个底面为正方形的四棱锥,其三视图如图所示,若这个四棱锥的体积为2,则此四棱锥最长的侧棱长为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{11}$ | C. | $\sqrt{13}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,在所有棱长均为1的四面体DEFG内有一个内接三棱柱ABC-A1B1C1,A,B,C在平面EFG内,A1,B1、C1分别在DE,DF,DG上,且AB=BC=CA=AA1,AA1⊥平面ABC,则AB=$\sqrt{6}$-2.
如图所示,在所有棱长均为1的四面体DEFG内有一个内接三棱柱ABC-A1B1C1,A,B,C在平面EFG内,A1,B1、C1分别在DE,DF,DG上,且AB=BC=CA=AA1,AA1⊥平面ABC,则AB=$\sqrt{6}$-2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}}$) | B. | (${\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29尺 | B. | 24尺 | C. | 26尺 | D. | 30尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
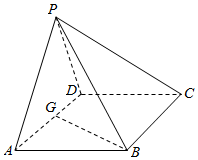 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin3>sin2 | B. | cos3>cos2 | C. | cos(-$\frac{2}{5}$π)<cos(-$\frac{1}{4}$π) | D. | sin$\frac{12}{5}$π<sin$\frac{17}{4}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com