
分析 容易知道分母恒大于0,得到分子要恒大于0.
解答 解:${a}^{2}-a+1=(a-\frac{1}{2})^{2}+\frac{3}{4}>0$,
∴1+2x+4xa>0,设t=2x,因为x∈(-∞,1],所以0<t≤2.
y=1+t+at2,要使y>0恒成立,即y=1+t+at2>0,所以$;a>-\frac{1+t}{{t}^{2}}$.
设$;f(t)=-(\frac{1}{t})^{2}-\frac{1}{t}$,则$;f(t)=-(\frac{1}{t}+\frac{1}{2})^{2}+\frac{1}{4}$,因为0<t≤2,所以$\frac{1}{t}≥\frac{1}{2}$,
所以$;{y}_{max}=-\frac{3}{4}$,所以a>-$-\frac{3}{4}$.
故答案为:(-$\frac{3}{4}$,+∞).
点评 本题考查了与指数函数有关的复合函数的最值问题,通过换元,将函数转化为一元二次函数,是解决本题的关键,对应不等式恒成立问题通常是转化为含参问题恒成立,即求函数的最值问题


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
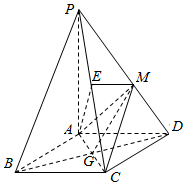 如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AD,点M是PD的中点,作ME⊥PC,交PC于点E.
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=AD,点M是PD的中点,作ME⊥PC,交PC于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,在所有棱长均为1的四面体DEFG内有一个内接三棱柱ABC-A1B1C1,A,B,C在平面EFG内,A1,B1、C1分别在DE,DF,DG上,且AB=BC=CA=AA1,AA1⊥平面ABC,则AB=$\sqrt{6}$-2.
如图所示,在所有棱长均为1的四面体DEFG内有一个内接三棱柱ABC-A1B1C1,A,B,C在平面EFG内,A1,B1、C1分别在DE,DF,DG上,且AB=BC=CA=AA1,AA1⊥平面ABC,则AB=$\sqrt{6}$-2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29尺 | B. | 24尺 | C. | 26尺 | D. | 30尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
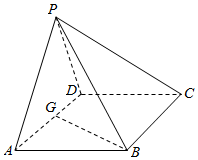 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 2 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com