练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)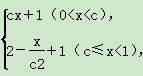＝且满足f(c2)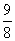＝，其中0＜c＜1.

    (1)求常数c的值；

    (2)解不等式f(x)>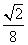＋1.

    难点突破


    (1)c＝

    (2)不等式f(x)>＋1的解集为)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若α，β是两个不同的平面，下列四个条件：

    ①存在一条直线a，a⊥α，a⊥β；

    ②存在一个平面γ，γ⊥α，γ⊥β；

    ③存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α；

    ④存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α．

    那么可以是α∥β的充分条件有（　C　）

    　 A． 4个 B． 3个 C． 2个 D． 1个

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝log36，b＝log510，c＝log714，则(　　)

    A. c>b>a       B. b>c>a         C. a>c>b            D. a>b>c

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ax2＋bx＋1(a，b∈R)，x∈R.

    (1)若函数f(x)的最小值为f(－1)＝0，求f(x)的解析式，并写出单调区间；

    (2)在(1)的条件下，f(x)>x＋k在区间[－3，－1]上恒成立，试求k的范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知函数f(x)＝若f(2m－1)<，则m的取值范围是(　　)

    A．m>  B．m<

    C．0≤m<  D.<m≤1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝的值域是(　　)

    A．[0，＋∞)  B．[0，2]

    C．[0，2)  D．(0，2)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝()x－log2(x＋2)在区间[－1，1]上的最大值为(　　)

    A．1  B．3  C．4  D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     定义在R上的函数f(x)是偶函数，且f(x)＝f(2－x)．若f(x)在区间[1，2]上是减函数，则f(x)(　　)

    A．在区间[－2，－1]上是增函数，在区间[3，4]上是增函数

    B．在区间[－2，－1]上是增函数，在区间[3，4]上是减函数

    C．在区间[－2，－1]上是减函数，在区间[3，4]上是增函数

    D．在区间[－2，－1]上是减函数，在区间[3，4]上是减函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设a＝log2.83.1，b＝logπe，c＝logeπ，则(　　)

    A．a<c<b  B．c<a<b

    C．b<a<c  D．b<c<a

    查看答案和解析>>

    同步练习册答案