
分析 (1)直接由数列递推式结合a1=1求得a2,a3,a4的值,猜测an,然后利用数学归纳法证明;
(2)比较3an与(n-1)2n+2n2的大小,即比较3n与(n-1)2n+2n2的大小,通过比较n=1,2,3,4,5时,两个代数式的大小,猜想结论,利用数学归纳法证明即可.
解答 解:(1)由an+1=$\frac{(n+2){a}_{n}^{2}-{na}_{n}+n+1}{{a}_{n}^{2}+1}$,且a1=1,
得${a}_{2}=\frac{3×{1}^{2}-1×1+2}{2}=2$,
${a}_{3}=\frac{4×{2}^{2}-2×2+3}{5}=3$,
${a}_{4}=\frac{5×{3}^{2}-3×3+4}{10}=4$.
由上猜测an=n.
下面用归纳法证明:
当n=1时,a1=1,结论成立;
假设当n=k时结论成立,即ak=k,
则当n=k+1时,${a}_{k+1}=\frac{(k+2)•{{a}_{k}}^{2}-k{a}_{k}+k+1}{{{a}_{k}}^{2}+1}$=$\frac{(k+2)•{k}^{2}-{k}^{2}+k+1}{{k}^{2}+1}$
=$\frac{{k}^{3}+{k}^{2}+k+1}{{k}^{2}+1}=\frac{k({k}^{2}+1)+{k}^{2}+1}{{k}^{2}+1}=\frac{(k+1)({k}^{2}+1)}{{k}^{2}+1}=k+1$.
∴当n=k+1时,结论成立.
综上,an=n;
(2)3an =3n,
当n=1时,3n>(n-1)2n+2n2;
当n=2,3时,3n<(n-1)2n+2n2;
当n=4,5时,3n>(n-1)2n+2n2
猜想:当n≥4时,3n>(n-1)2n+2n2,
下面用数学归纳法证明:
由上述过程可知,n=4时结论成立,
假设当n=k,(k≥4)时结论成立,即3k>(k-1)2k+2k2,
两边同乘以3得:3k+1>3[(k-1)2k+2k2]=k2k+1+2(k+1)2+[(k-3)2k+4k2-4k-2].
而(k-3)2k+4k2-4k-2=(k-3)2k+4(k2-k-2)+6=(k-3)2k+4(k-2)(k+1)+6>0.
∴3k+1>((k+1)-1)2k+1+2(k+1)2 .
即n=k+1时结论也成立,
∴当n≥4时,3n>(n-1)2n+2n2成立.
点评 本题考查数列递推式,考查了数列的函数特性,训练了利用数学归纳法证明与自然数有关的命题,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
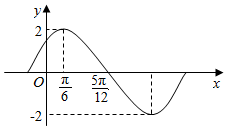 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0、|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0、|φ|<$\frac{π}{2}$)的图象的一部分如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<-1 | B. | 0<m<1 | C. | m>1 | D. | m≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com