
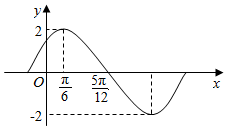
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0、|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0、|φ|<$\frac{π}{2}$)的图象的一部分如图所示.分析 (1)由题意求出A,T,利用周期公式求出ω,利用当x=$\frac{π}{6}$时取得最大值2,求出φ,即可得到函数的解析式,进而可求其单调递增区间.
(2)令f(x)=g(x),分类讨论,利用正弦函数的图象和性质即可解得交点的坐标.
解答 解:(1)由题意可知A=2,T=4×($\frac{5π}{12}$-$\frac{π}{6}$)=π=$\frac{2π}{ω}$,解得ω=2,
因为:当x=$\frac{π}{6}$时取得最大值2,
所以:2=2sin(2×$\frac{π}{6}$+φ),可得:2×$\frac{π}{6}$+φ=2kπ+$\frac{π}{2}$,k∈Z,解得:φ=2kπ+$\frac{π}{6}$,k∈Z,
因为:|φ|<$\frac{π}{2}$,
所以:φ=$\frac{π}{6}$,
所以:函数f(x)的解析式:f(x)=2sin(2x+$\frac{π}{6}$).
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,可得:kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z,
所以:函数f(x)的单调递增区间为:[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z,
因为:x∈[0,π],
所以:函数f(x)在[0,π]上的单调递增区间为:[0,$\frac{π}{6}$],[$\frac{2π}{3}$,π].
(2)∵f(x)=2sin(2x+$\frac{π}{6}$),g(x)=$\left\{\begin{array}{l}{1(0<x<π)}\\{\frac{1}{2}(x=π)}\\{0(π<x<2π)}\end{array}\right.$,
∴分类讨论:
①当0<x<π时,由2sin(2x+$\frac{π}{6}$)=1,可得sin(2x+$\frac{π}{6}$)=$\frac{1}{2}$,解得:2x+$\frac{π}{6}$=2kπ+$\frac{5π}{6}$,k∈Z,即x=kπ+$\frac{π}{3}$,k∈Z,从而解得其交点坐标为:($\frac{π}{3}$,1).
②当x=π时,f(π)=2sin(2π+$\frac{π}{6}$)=1,g(π)=$\frac{1}{2}$,无交点.
③当π<x<2π时,由2sin(2x+$\frac{π}{6}$)=0,可得:2x+$\frac{π}{6}$=kπ,k∈Z,即x=$\frac{kπ}{2}$-$\frac{π}{12}$,k∈Z,
由于π<x<2π,可得2个交点的坐标分别为:($\frac{17π}{12}$,0),($\frac{23π}{12}$,0).
点评 本题给出函数y=Asin(ωx+φ)的部分图象,要我们确定其解析式并求函数图象与g(x)的交点坐标,着重考查了三角恒等变换和三角函数的图象与性质等知识点,注意函数的周期的求法,考查计算能力,常考题型,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [${\frac{π}{6}$,$\frac{5π}{6}}$] | B. | [${\frac{π}{3}$,$\frac{2π}{3}}$] | C. | [0,$\frac{π}{6}}$]∪[${\frac{5π}{6}$,π] | D. | [0,$\frac{π}{3}}$]∪[${\frac{2π}{3}$,π] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 每批试验菜籽数(n) | 2 | 5 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 |
| 发芽菜籽数(m) | 2 | 4 | 9 | 60 | 116 | 282 | 639 | 1139 | 1806 | 2715 |
| 发芽频率($\frac{m}{n}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com