
| 每批试验菜籽数(n) | 2 | 5 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 |
| 发芽菜籽数(m) | 2 | 4 | 9 | 60 | 116 | 282 | 639 | 1139 | 1806 | 2715 |
| 发芽频率($\frac{m}{n}$) |
分析 根据表中信息,用发芽的粒数除以每批粒数,得到频率,由于试验次数较多,可以用频率估计概率
解答 解:(1)在相同的条件下,对某种油菜籽进行发芽试验,结果如表:
| 每批试验菜籽数(n) | 2 | 5 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 |
| 发芽菜籽数(m) | 2 | 4 | 9 | 60 | 116 | 282 | 639 | 1139 | 1806 | 2715 |
| 发芽频率($\frac{m}{n}$) | 1 | 0,8 | 0.9 | 0.857 | 0.892 | 0.910 | 0.913 | 0.757 | 0.903 | 0.905 |
点评 本题主要考查利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{2}}{4π}$ | B. | $\frac{4π-3\sqrt{2}}{4π}$ | C. | $\frac{1}{2π}$ | D. | $\frac{2π-1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
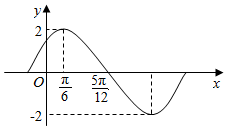 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0、|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0、|φ|<$\frac{π}{2}$)的图象的一部分如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<-1 | B. | 0<m<1 | C. | m>1 | D. | m≥1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com