
分析 (1)设AB的方程为为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),可得$\frac{2}{a}$+$\frac{1}{b}$=1,利用基本不等式算出ab≥8,可得当且仅当a=4且b=2时,△AOB的面积S有最小值为4,进而算出此时的直线l方程;
(2)过P作PC⊥x轴于点C,PD⊥y轴于点D,设∠PAO=θ,利用解直角三角形知识算出|AC|,|BD|=2tanθ,从而将|OA|+|OB|表示为关于tanθ的式子,再利用基本不等式加以计算,即可求出|OA|+|OB|的最小值,而此时直线斜率为-$\frac{\sqrt{2}}{2}$,利用点斜式方程列式,化简可得直线l的方程.
(3)由(2)的结论得|PA|,|PB|,利用二倍角的正弦公式算出|PA|•|PB|,由正弦函数的值域可得当θ=$\frac{π}{4}$时,|PA|•|PB|取最小值4.而此时直线斜率为-1,利用点斜式方程列式,化简可得直线l的方程.
解答 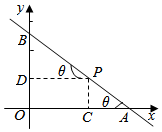 解:(1)设直线AB的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),
解:(1)设直线AB的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),
∵点P(2,1)在直线上,
∴$\frac{2}{a}$+$\frac{1}{b}$=1,
由基本不等式1=$\frac{2}{a}$+$\frac{1}{b}$≥2$\sqrt{\frac{2}{a}•\frac{1}{b}}$=$\sqrt{\frac{8}{ab}}$,当且仅当a=4且b=2时,等号成立,
∴ab≥8,可得△AOB的面积S=$\frac{1}{2}$ab≥4,
因此△AOB的面积S的最小值为4,
此时的直线方程为$\frac{x}{4}$+$\frac{y}{2}$=1,即x+2y-4=0;
(2):设∠PAO=θ,则可得θ∈(0,$\frac{π}{2}$),
过P作PC⊥x轴于点C,PD⊥y轴于点D,
则Rt△PDB中,tanθ=$\frac{|BD|}{|PD|}$,可得|BD|=|PD|tanθ=2tanθ,
cosθ=$\frac{|PD|}{|PB|}$,可得|PB|=$\frac{|PD|}{cosθ}$=$\frac{2}{cosθ}$,
同理,在Rt△PAC中,有|AC|=$\frac{|PC|}{tanθ}$=$\frac{1}{tanθ}$,|PA|=$\frac{1}{sinθ}$,
∴|OA|+|OB|=|OC|+|AC|+|OD|+|BD|=3+$\frac{1}{tanθ}$+2tanθ,
∵θ∈(0,$\frac{π}{2}$),得tanθ>0,
∴$\frac{1}{tanθ}$+2tanθ≥2$\sqrt{2}$,可得当且仅当tanθ=$\frac{\sqrt{2}}{2}$时,等号成立.
由此可得|OA|+|OB|的最小值为3+2$\sqrt{2}$,
此时方程为的斜率为-$\frac{\sqrt{2}}{2}$,
直线l的方程为y-1=-$\frac{\sqrt{2}}{2}$(x-2),化为一般式可得$\sqrt{2}$x+2y-2-2$\sqrt{2}$=0
(3)∵|PA|=$\frac{1}{sinθ}$,|PB|=$\frac{2}{cosθ}$,
∴|PA|•|PB|=$\frac{4}{sin2θ}$
当2θ=$\frac{π}{2}$,即θ=$\frac{π}{4}$时,|PA|•|PB|取最小值4,
此时,直线的倾斜角为$\frac{3π}{4}$,斜率为-1,
直线l的方程为y-1=-1(x-2),化为一般式可得x+y-3=0
点评 本题给出直线经过定点,求满足特殊条件的直线方程,着重考查了直线的基本量与基本形式、三角形面积的计算和基本不等式求最值等知识,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
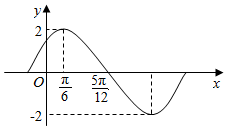 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0、|φ|<$\frac{π}{2}$)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0、|φ|<$\frac{π}{2}$)的图象的一部分如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com