
【题目】已知函数![]() .
.
(1)证明:![]() ,
,![]() ;
;
(2)判断![]() 的零点个数,并给出证明过程.
的零点个数,并给出证明过程.
【答案】(1)证明见解析;(2)三个零点,证明见解析.
【解析】
(1)由函数![]() 是偶函数,只需利用导数证明函数
是偶函数,只需利用导数证明函数![]() 在区间
在区间![]() 上的最大值
上的最大值![]() 即可;
即可;
(2)由(1)得出函数![]() 在区间
在区间![]() 上只有一个零点,然后利用函数值符号得出该函数在区间
上只有一个零点,然后利用函数值符号得出该函数在区间![]() 上无零点,利用导数分析函数的单调性,并分析极值的符号,结合零点存在定理得出该函数在区间
上无零点,利用导数分析函数的单调性,并分析极值的符号,结合零点存在定理得出该函数在区间![]() 上有且只有一个零点,由偶函数的性质得出该函数在区间
上有且只有一个零点,由偶函数的性质得出该函数在区间![]() 上也只有一个零点,从而得出函数
上也只有一个零点,从而得出函数![]() 有三个零点.
有三个零点.
(1)![]() ,
,![]() ,则该函数为偶函数,
,则该函数为偶函数,
只需证![]() ,其中
,其中![]() .
.
![]() ,
,![]() .
.
当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递增.
单调递增.
![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递减,则
单调递减,则![]() ,
,
因此,对任意的![]() ,
,![]() ;
;
(2)三个零点,证明如下:
由(1)可知,当![]() 时,函数
时,函数![]() 有一个零点
有一个零点![]() .
.
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 无零点;
无零点;
当![]() 时,
时,![]() ,
,![]() .
.
此时,函数![]() 单调递增,
单调递增,![]() ,
,![]() .
.
由零点存在定理可知,存在![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 单调递增.
单调递增.
![]() ,
,![]() ,
,![]() .
.
由零点存在定理知,函数![]() 在区间
在区间![]() 上无零点,在区间
上无零点,在区间![]() 上有且只有一个零点,即函数
上有且只有一个零点,即函数![]() 在区间
在区间![]() 上有且只有一个零点.
上有且只有一个零点.
由于函数![]() 为偶函数,所以,函数
为偶函数,所以,函数![]() 在
在![]() 上无零点,在
上无零点,在![]() 上有且只有一个零点.
上有且只有一个零点.
综上所述,函数![]() 有三个零点.
有三个零点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为![]() |OB|.
|OB|.
(1)求椭圆C的方程;
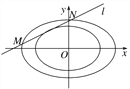
(2)如图,若椭圆![]() ,椭圆
,椭圆![]() ,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
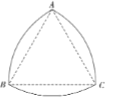
【题目】勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为( )
A.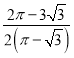 B.
B.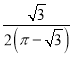
C.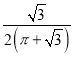 D.
D.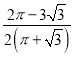
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
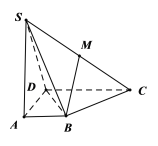
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)![]() 为
为![]() 中点,在四边形
中点,在四边形![]() 所在的平面内是否存在一点
所在的平面内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求三角形
,若存在,求三角形![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调研机构,对本地![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有
人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有![]() 人为“低碳族”,该
人为“低碳族”,该![]() 人的年龄情况对应的频率分布直方图如图.
人的年龄情况对应的频率分布直方图如图.

(1)根据频率分布直方图,估计这![]() 名“低碳族”年龄的平均值,中位数;
名“低碳族”年龄的平均值,中位数;
(2)若在“低碳族”且年龄在![]() 、
、![]() 的两组人群中,用分层抽样的方法抽取
的两组人群中,用分层抽样的方法抽取![]() 人,试估算每个年龄段应各抽取多少人?
人,试估算每个年龄段应各抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,若点A为函数
,若点A为函数![]() 上的任意一点,点B为函数
上的任意一点,点B为函数![]() 上的任意一点.
上的任意一点.
(1)求A,B两点之间距离的最小值;
(2)若A,B为函数![]() 与函数
与函数![]() 公切线的两个切点,求证:这样的点B有且仅有两个,且满足条件的两个点B的横坐标互为倒数.
公切线的两个切点,求证:这样的点B有且仅有两个,且满足条件的两个点B的横坐标互为倒数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“韩信点兵”问题在我国古代数学史上有不少有趣的名称,如“物不知数”“鬼谷算”“隔墙算”“大衍求一术”等,其中《孙子算经》中“物不知数”问题的解法直至1852年传由传教士传入至欧洲,后验证符合由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. 原文如下:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”这是一个已知某数被3除余2,被5除余3,被7除余2,求此数的问题.现将1至2017这2017个数中满足条件的数按由小到大的顺序排成一列数,则中位数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名的![]() 周髀算经
周髀算经![]() 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷![]() 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸![]() 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为![]() 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分![]() 则“立春”时日影长度为
则“立春”时日影长度为![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com