
分析 (1)由$x=\frac{t+1}{t-1}$,解得t=$\frac{x+1}{x-1}$,代入y=$\frac{2t}{{t}^{3}-1}$化简即可得出,注意定义域.
(2)$\left\{\begin{array}{l}{x=3+15cosθ}\\{y=2+15sinθ}\end{array}\right.$(0≤θ<2π),利用cos2θ+sin2θ=1化简即可得出,注意取值范围.
解答 解:(1)由$x=\frac{t+1}{t-1}$,解得t=$\frac{x+1}{x-1}$,
代入y=$\frac{2t}{{t}^{3}-1}$可得:y=$\frac{\frac{2(x+1)}{x-1}}{(\frac{x+1}{x-1})^{3}-1}$,
化为y=$\frac{(x+1)(x-1)^{2}}{3{x}^{2}+1}$.
另一方面:由$x=\frac{t+1}{t-1}$=1+$\frac{2}{t-1}$≠1,
∴y=$\frac{(x+1)(x-1)^{2}}{3{x}^{2}+1}$的定义域是{x|x∈R,x≠1}.
∴y=$\frac{(x+1)(x-1)^{2}}{3{x}^{2}+1}$,x∈{x|x∈R,x≠1}.
(2)$\left\{\begin{array}{l}{x=3+15cosθ}\\{y=2+15sinθ}\end{array}\right.$(0≤θ<2π),
可得(x-3)2+(y-2)2=225(x∈[-12,18],y∈[-13,17]).
点评 本题考查了参数方程化为普通方程、平方关系,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<a≤3 | B. | a>2 | C. | 1<a<2 | D. | 2<a≤3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
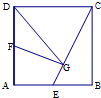 如图所示,正方形ABCD的边长为2,E,F分别为AB,AD的中点,G为线段CE上的一个动点,设$\frac{CG}{CE}$=x,S△GDF=y,则函数y=f(x)的图象大致是( )
如图所示,正方形ABCD的边长为2,E,F分别为AB,AD的中点,G为线段CE上的一个动点,设$\frac{CG}{CE}$=x,S△GDF=y,则函数y=f(x)的图象大致是( )| A. | 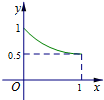 | B. | 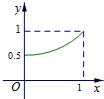 | C. | 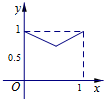 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )| A. | O-ABC是正三棱锥(底面为正三角形,顶点在底面的投影为底面的中心) | |
| B. | 直线OB∥平面ACD | |
| C. | OD⊥平面ABC | |
| D. | 直线CD与平面ABC所成的角的正弦值为$\frac{{\sqrt{6}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com